

―二次元材料・ヘテロ構造まで網羅―
量子コンピューター向け材料を見分ける新しい方法を発見しました。
東北大学の金井駿准教授、米国シカゴ大学及び米国アルゴンヌ国立研究所のジューリア ガリ教授、マイケル トリヤマ博士らの研究チームは、材料内部の磁気的な揺らぎが量子状態を乱す仕組みに注目し、計算科学を使って量子状態の安定性を高速に予測する手法を開発しました。
特に、従来は三次元の材料のみが評価可能でしたが、今回、二次元材料や積層構造まで解析を広げることで、より実在材料に近い環境で量子状態の安定性を予測することに成功しました。約千種類の候補から190種類の有望な材料を抽出し、中でも代表的な二次元材料である二硫化タングステン(WS2)では、きわめて長い時間(35ミリ秒(ミリ秒は1000分の1秒))量子状態が持続することを予測しました。
この手法は、数万種類規模の新材料設計にも応用でき、将来的には量子コンピューターの心臓部となる素子や、超高感度な量子センサーの開発を大きく前進させることが期待されます。
本成果は2025年11月26日付で、npj 2D Materials and Applicationsに掲載されました。
量子コンピューターをはじめとする次世代の量子技術は、これまでの計算機の限界を超える新しい情報処理の実現を目指しています。物質の中で量子状態がどれだけ安定して保たれるか、つまり量子状態の安定性が保たれる時間(T2)(注2)が、量子ビットとしての性能を左右する鍵とされています。
図1にT2を実材料で計算するための研究の歴史をまとめました。量子の世界を支配する基本原理が形になったのは、今からおよそ100年前のことです。1925年から26年にかけて、シュレディンガー方程式とハイゼンベルグ方程式が発表され、物質の量子状態を記述する理論の枠組みが整いました。
それ以来、物質の中で量子状態がどれだけ安定して保たれるかを定量的に理解することが、量子技術の発展において中心的なテーマとなってきました。1970年代には、T2を理論的に計算する方法が提案されましたが、実際の材料では膨大な行列計算(注3)が必要で、現実的な予測はほとんど不可能でした。2000年代に入ってようやく、小さな行列を繰り返し計算する近似的な手法が登場しますが、それでも1つの材料を解析するのに数分から数日を要しました。
転機となったのが2021年です。東北大学の金井駿准教授、大野英男総長(当時)とシカゴ大学及びアルゴンヌ国立研究所(ともに米国)のデイビッド オーシュロム教授、ジューリア ガリ教授の研究チームが、三次元材料についてT2を単純な四則演算と累乗計算で求められる「一般化スケーリング則」を発見し、量子状態の安定性を誰でも容易に予測できる仕組みを示しました(参考文献1、参考文献2)。この理論的指針をもとに多くの実験研究が行われ、世界中でその再現が確認されています。
これまで、量子状態の安定性に関する研究は三次元材料を中心に進められてきました。一方、原子層レベルで人工的に設計できる二次元材料や、それらを組み合わせたヘテロ接合構造では、同様の手法で安定性を評価することが難しく、統一的な理論は存在していませんでした。近年、こうした二次元材料やヘテロ接合は、エレクトロニクスや量子情報処理への応用を目指して世界的に研究が活発化しています。
この課題に対し、東北大学電気通信研究所の金井駿准教授、シカゴ大学及びアルゴンヌ国立研究所のマイケル トリヤマ博士、ジューリア ガリ教授、ジーウェイ ザン博士の研究チームは、量子状態の安定性を高精度かつ高速に予測できる新しい理論計算手法を開発しました。研究チームは、材料中の原子核の磁気的な揺らぎがスピン量子ビットの安定性を支配することに着目し、この相互作用を解析するクラスター相関展開法(CCE)(注4)を自動化しました。これを高スループット計算とデータ駆動モデルに組み合わせることで、材料ごとの量子状態の保持時間(T2)を網羅的に予測できる枠組みを確立しました。
まず二次元材料については、1173種類の候補の中からT2が1ミリ秒よりも大きい材料、190種類を同定しました。中でもWS2は、トランジスタや発光デバイス、光検出器などに用いられる代表的な二次元半導体であり、今回の解析でT2 = 35ミリ秒という極めて長い量子状態の安定性を示しました。すでにスピン量子ビットとしての実験報告もあり、WS2はエレクトロニクスと量子情報をつなぐ共通基盤材料として新たな可能性を示しました。この成果により、実在する二次元材料群の中で、量子状態の安定性を左右する要因と設計指針が初めて体系的に明らかになりました(図2)。
この新しい関係を代数的に整理することで、三次元材料に対して2021年に発見された「一般化スケーリング則」を二次元材料およびヘテロ接合系にまで拡張することに成功しました(図3)。これにより、三次元材料・二次元材料・ヘテロ接合材料のすべての実在材料系に対して、量子状態の安定性を統一的に表現・予測できる理論的枠組みが完成しました。
本成果は、量子情報科学と最先端材料科学をつなぐ新たな橋渡しとなるものです。
今回確立した理論と計算手法は、今後の量子技術開発に幅広い波及効果をもたらします。まず、理論的には、三次元・ヘテロ接合・二次元を貫く統一的な「量子状態の安定性スケーリング則」を確立したことで、材料科学と量子情報科学を結ぶ新しい共通基盤が生まれました。これにより、理論計算だけでなく、実験グループや産業界が利用できる量子材料設計の標準指針として機能します。実際の応用に向けた次のステップは、三次元材料で実験実証されつつあるこうした新たな色中心スピン量子ビット向け材料の実証に加えて(参考文献3)、今回の枠組みに基づき、理論で予測した高安定材料を実際に合成し、スピン共鳴測定や光学計測によりT2の直接実証を進めることです。
また、今回確立した枠組みは、量子コンピューターの演算精度を高めるだけでなく、高感度な量子磁気センサーや量子通信デバイスの長寿命化など、量子技術全体の信頼性向上につながります。さらに、低ノイズ基板設計の指針を共有することで、半導体・材料メーカーとの共同開発を促し、既存製造技術と両立可能な量子デバイスプラットフォームの構築を目指します。将来的には、東北大学とシカゴ大学を中心とした国際共同研究のもと、理論・実験・産業を横断した「量子材料設計エコシステム」を形成し、量子情報社会の実現に向けた学際的研究をさらに推進していく予定です。
東北大学はシカゴ大学との海外サテライト協定を結んでおり、金井准教授を日本側の代表としてジョイントリサーチセンターを推進しています。
また東北大学とシカゴ大学は量子研究に関して、“Chicago-Tohoku Quantum Alliance”(注5)を2023年に締結し、共同研究を推進しています(参考文献4)。
共同研究の一層の強化により、さらなる世界的成果の創出が期待されます。
本研究の一部は、JST戦略的創造研究推進事業さきがけ(課題番号:JPMJPR21B2)、JSPS科研費(課題番号:JP23KK0092)、QST-SIPプログラム、東北大学新領域創成のための挑戦研究デュオの支援を受けて行われたものです。


 (注5)
(注5)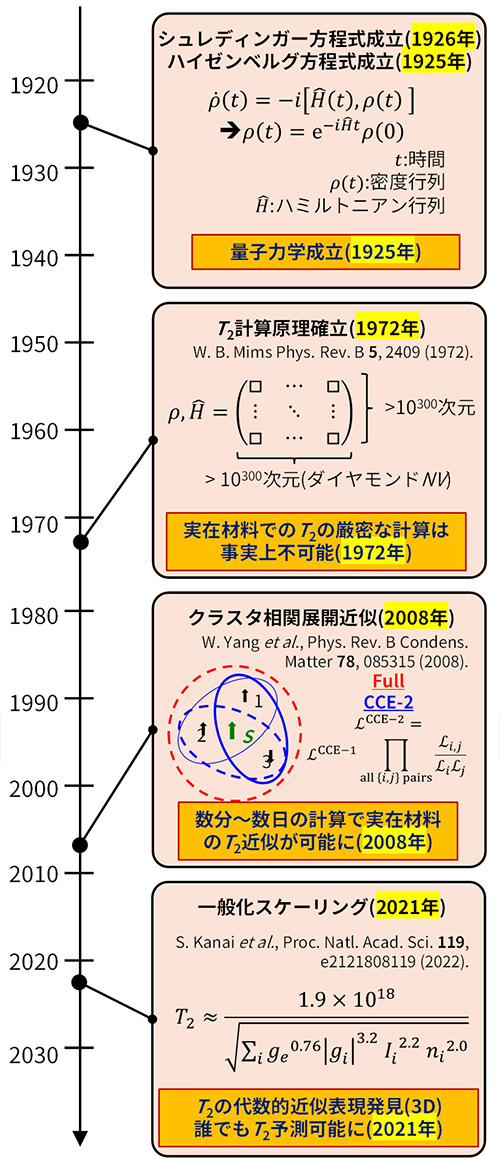
図1. 位相緩和時間(T2)の計算研究の発展史
1925~26年に量子力学の基礎方程式(シュレディンガー方程式・ハイゼンベルグ方程式)が確立した。1972年にT2計算の理論原理が提案されたものの、実在材料では膨大な行列計算のため実用的な解析は困難だったが、2008年にクラスター相関展開法(CCE)により実用的な近似計算が可能となった。2021年に東北大学・シカゴ大学の共同研究により、三次元材料のT2を代数的に表現できる「一般化スケーリング則」が発見された。本研究はこの理論を二次元およびヘテロ構造材料へと拡張するものである。
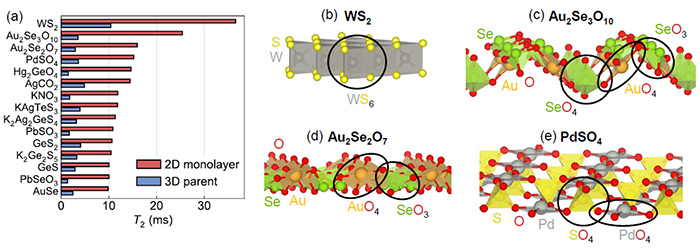
図2. 高T2の二次元材料の例と三次元母体材料のT2の比較
(a)より、三次元材料と比較して、二次元材料において長いT2が予測されることがわかる。(b)-(e)にT2が比較的長い二次元材料の例を示す。WS2のようなすでに量子ビットとして応用されている材料に加えて、量子ビットとしての性能が確かめられていない新たな材料系が提案された。
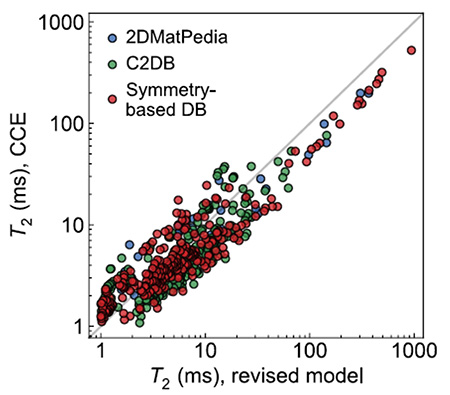
図3. T2の理論式による予測と大規模行列計算の比較
二次元系に対するT2の代数的表現による理論式と大規模行列計算の比較結果。グレーの薄い線が予測結果であり、おおむね理論式で計算結果を表すことができることを示している。
| タイトル: | Strategies to search for two-dimensional materials with long spin qubit coherence time |
|---|---|
| 著者: | Michael Y. Toriyama, Jiawei Zhan, Shun Kanai, Giulia Galli |
| 掲載誌: | npj 2D Materials and Applications |
| DOI: | 10.1038/s41699-025-00623-8 |
東北大学電気通信研究所
准教授 金井 駿(研究者プロフィール)
(兼)東北大学大学院工学研究科電子工学専攻
(兼)東北大学先端スピントロニクス研究開発センター(CSIS)
(兼)東北大学高等研究機構 新領域創成部
(兼)東北大学材料科学高等研究所(WPI-AIMR)
(兼)量子科学技術研究開発機構(QST)
| Tel: | 022-217-5555 |
|---|---|
| E-mail: | skanai@tohoku.ac.jp |
東北大学電気通信研究所 総務係
| Tel: | 022-217-5420 |
|---|---|
| E-mail: | riec-somu@grp.tohoku.ac.jp |
科学技術振興機構 広報課
| Tel: | 03-5214-8404 |
|---|---|
| E-mail: | jstkoho@jst.go.jp |
科学技術振興機構 戦略研究推進部 グリーンイノベーショングループ
安藤 裕輔
| Tel: | 03-3512-3526 |
|---|---|
| E-mail: | presto@jst.go.jp |
東北大学材料科学高等研究所 国際推進係
| Tel: | 022-217-5971 |
|---|---|
| E-mail: | iac@grp.tohoku.ac.jp |
東北大学グローバル戦略室
| Tel: | 022-217-6311 |
|---|---|
| E-mail: | kokusai-r@grp.tohoku.ac.jp |