固体中の量子情報の保持時間を記述する法則を発見
固体中の量子情報の保持時間を記述する法則を発見
~誰でも短時間で量子ビット材料探索が可能に~
発表のポイント
- 量子ビットとして使われる固体中のスピン中心注1)の性能を決める位相緩和時間(量子情報を保持可能な時間、T2)注2)を支配する「一般化スケーリング則」を発見した。これにより、実用材料中のスピンの量子状態に関する、半世紀にわたる未解決問題の解決に成功した
- 従来は複雑・大規模な計算により、1つの材料につき最大数日を要したT2予測計算が、関数電卓などのありふれたツールで瞬時に実行可能になった
- 12,000種を超える候補材料についてT2を調べ、量子ビットの性能を向上することが予測される700種以上の新しい量子材料を予測した
- 「ニューノーマル」の時代及び「Society5.0」での活躍が期待される、従来技術では困難な問題解決を拓く量子コンピューター注3)などの量子デバイス材料研究を加速
概要
固体中のスピン中心は、量子ビット注3)を構成する物理系の1つで、量子テレポーテーションなどが実証された他、一部が室温動作可能であるという特長により大きく注目されています。
東北大学電気通信研究所の金井駿助教と大野英男教授(現総長)は、シカゴ大学及びアルゴンヌ研究所(米国)のDavid D. Awschalom教授を中心とする研究グループとの共同研究により、固体中のスピン中心の量子ビットとしての性能を決める、位相緩和時間(T2)を支配する「一般化スケーリング則」を発見しました。これにより、『実材料のT2を記述することはできるか?』という量子スピン物理研究50年来の問題を解決すると同時に、12,000種を超える材料のT2予測に本発見を応用することで、新たな量子ビット材料の大規模かつ定量的な材料探索を行いました。本研究成果は、次世代の量子材料研究、新奇量子物性の探索に関する研究を基礎・応用の両面から大きく加速させるものです。
本成果は2022年4月6日付で米国の科学誌「Proceedings of the National Academy of Sciences of the United States of America」で公開されました。
背景 ― 量子ビット、位相緩和時間、固体中のスピン中心を用いた量子ビット ―
量子ビット注2)と呼ばれる「0かつ1」という複数の情報を重ね合わせて保持・計算可能な情報媒体が提案されています。量子情報を重ね合わせて保持可能な時間は位相緩和時間(T2)と呼ばれ、T2は量子ビットとしての性能を決定づける重要な指標の一つです。固体中のスピン中心は量子ビットを構成する物理系の一つで、その代表例はダイヤモンド窒素-空孔(NV)中心注1)です。ダイヤモンドNV中心を用いた量子ビットは主に光とマイクロ波により操作されます。量子ビットの操作手法は母体材料の物性と密接に関連し、母体材料の探索により新しい操作手法を見出し、より高度・高効率な量子計算の実現に対する機運が高まっています(量子ビットに適した固体中のスピン中心は?~ブレイクスルーへ向けた物性・材料の探索指針~注4))。
母体材料選定の項目としてもT2は重要です。例えば、ダイヤモンド中のT2はさまざまな周囲環境からの熱的、磁気的、電気的相互作用(ノイズ)によって抑制されますが、高品質なダイヤモンド結晶であるほどこれらのノイズ源が減り、T2も長くなります。最高品質のダイヤモンドの場合、ダイヤモンドを構成する炭素原子のうち、天然に1%含まれる13C中の非常に微小な核スピン注3)からの磁気的ノイズがスピン中心のT2を決定します。T2はシュレーディンガー方程式注5)の時間発展計算により求められることが1960年代から知られていましたが、実際の材料でスピン中心と実効的に相互作用する核スピンは通常1,000個以上であることが知られ、そのT2を求めるためには大きさ21000×21000の巨大な行列の計算注6)が必要となります。従って、近年まで、実材料のT2は定量的な予測計算が不可能な量子物性でした。2008年、クラスター相関展開(CCE)注7)と呼ばれる近似手法をT2計算に用いることが提案されました。CCEでは上記の巨大な行列を最大で200×200程度の比較的小さな行列に分割し、分割した行列での計算を多数回繰り返すことでT2計算を実現します。CCEにより得られたT2の計算値は過去に得られた実験値と近いことが報告され、CCE計算の有効性が広く認識されるようになりつつあります。CCEに基づいた逐次的数値計算は、物質のT2を現実的な時間で計算することを可能とした一方で、1つの材料につき数分~数日の計算時間を要するため、大規模な材料探索への応用には課題がありました。
成果 ― 一般化スケーリング則の発見、大規模量子材料探索への応用 ―
今回、東北大学とシカゴ大学、アルゴンヌ研究所などからなる国際共同研究チームは、CCEに基づいて量子ビットに適した材料の大規模探索を行う手法を模索する下記過程(1)(2)で逐次的数値計算に頼ることなく、物質中のT2を計算することが可能なT2の代数的表現を発見しました。
- 同種の核スピン集合のT2の一般化スケーリング則 単一の核スピンの集合からなる母体材料の場合、そのT2には核スピンの①スピン量子数、②g因子注3)、③濃度及び、④電子スピン中心のg因子に対するスケーリング則が成立することを発見しました。図1は、ある母体材料中に単一の核スピンのみが存在していると仮定した場合の、CCEに基づいたT2計算の結果です。有限のスピン量子数を持つ125種の安定核種全てのT2が、核スピンのg因子×(スピン量子数)0.66という簡単な一つの代数式で表されること、即ち核スピンの①スピン量子数と②g因子に対するスケーリングを示しています。図1では③核スピン濃度と④電子スピンg因子は同一値としていますが、最終的にこれらに対するスケーリング関係も明らかにし、T2の核スピンの①スピン量子数、②g因子、③濃度及び、④スピン中心のg因子による「一般化スケーリング則」へと拡張することに成功しました。単体材料について簡単に知ることができる、①~④の4つの物理量が分かれば、行列計算なしで、かつ瞬時にT2が計算可能であることを意味します。
- 異種の核スピン集合間のデカップリング 我々の身の回りにある殆どの物質は化合物であり、異なる核スピン間の相互作用を考慮する必要があるため、(1)で得られた「単一核種に対する一般化スケーリング則」を実際の材料探索へ適用するにはもう一工夫必要です。研究グループは次に、化合物のT2を単一の核スピン集合のT2から簡単に構成する手法を発見しました。下記図2(上)のように、例えば、石英(SiO2)の場合、スピンを持つ原子核として、29Siと17Oが存在します。①同種の核スピンの相互作用のみ、②異種の核スピンの相互作用のみ、③全ての相互作用 を加味した場合の3種類の量子状態の保持量を示す指標(コヒーレンス)の計算の結果を図2(下)に示します。①と③がほぼ同じ傾向であることから、量子状態の消失には①同種の核スピンの相互作用 が支配的な影響を及ぼしていることが分かります。化合物中に含まれる全ての①同種核スピン集合によるT2を後から重ね合わせることにより、化合物のT2を計算することが可能であること、特に、この重ね合わせ手法に含まれる任意性が計算に与える誤差を詳細に検討し、材料に依存せず比較的良い精度で化合物のT2を求めることが可能である重ね合わせの手法を初めて示しました。
前述の通り、(1)と(2)を組み合わせることにより、化合物のT2を、逐次的大規模行列計算なしで予測することが可能です。天然存在比を持つ12,000を超える安定物質についてT2を予測した結果、比較的長い位相緩和時間の目安となる、1ミリ秒を超えるT2を持つと予測される材料が800種類以上存在することが分かりました。図3にその約800材料の内訳を示します。SiCを除いてはカルコゲナイド(酸化物、硫化物、セレン化合物、テルル化合物、及びそれらの複合化合物)に分類され、これらのほとんどは量子材料としては未踏です。さらに、SiCは最も長いT2を実験的に観測したSiCよりも長いT2を持つと予測される材料が700種以上の見つかり、今後固体中スピン中心の量子ビット応用に向けた材料探索に大きく貢献することが期待されます。
成果の意義と今後の展望
核スピンの相互作用下の電子スピンの量子状態に関する理論的研究は1960年代に端を発し、スピン系の量子ビットの基本原理です。本理論の究極の目的は、「身の回りの実用的な材料におけるT2を理論的に記述する」ことであり、本研究でこの50年来の問題解決に成功しました。また、これまで行列計算を用いて、1つ当たり何日も掛けて計算してきたT2を、関数電卓や表計算ソフトのようなありふれたツールで、瞬時に誰でも計算できるようになり、今後の量子材料探索を大幅に加速するブレイクスルーとなることが期待されます。
固体中のスピン中心の量子応用研究は、量子材料研究の進歩とともに日々新たな展開を迎えています。本研究で有望であることが示された酸化物材料は非常に多彩な機能性(物性制御の手法)を有することが知られる一方、これまで固体中のスピン中心を構成する材料としては主流ではありませんでした。ダイヤモンドやSiCに続く優れた量子ビット材料、特に酸化物やカルコゲナイドを用いた量子ビット研究の先駆けとなる可能性が大いに期待され、既存の量子材料以外の材料研究者や、企業関係者を参入させることにも一役買うことが考えられます。
本研究の一部は、丸文財団 交流研究助成、電気通信研究所 若手教員海外派遣プログラム、文部科学省 研究大学強化促進事業、日本学術振興会 科学研究費助成事業 国際共同研究強化(B)19KK0130、基盤研究(B)20H02178、科学技術振興機構 戦略的創造研究推進事業 さきがけ「不確定性スピントロニクスデバイス」(研究代表者:金井 駿)JPMJPR21B2などの支援を受けて行われたものです。また、東北大学はシカゴ大学との海外サテライト協定を結んでおり、本研究の推進により国際共同研究が一層強化され、さらなる世界的成果の創出が期待されます。
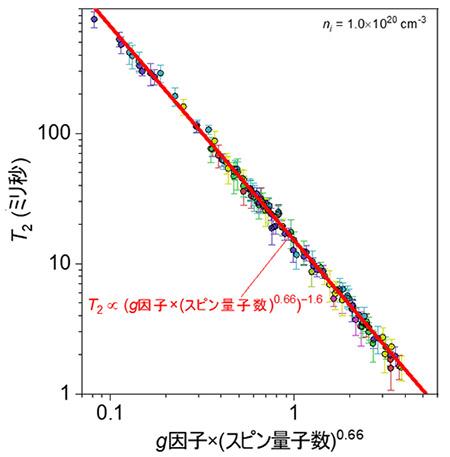
図1 単一核種により構成される材料におけるT2のスケーリング 有限のスピン量子数を有する125種の核種について計算したT2が核スピンのg因子とスピン量子数により単一のスケール則により表現されることを表した様子。
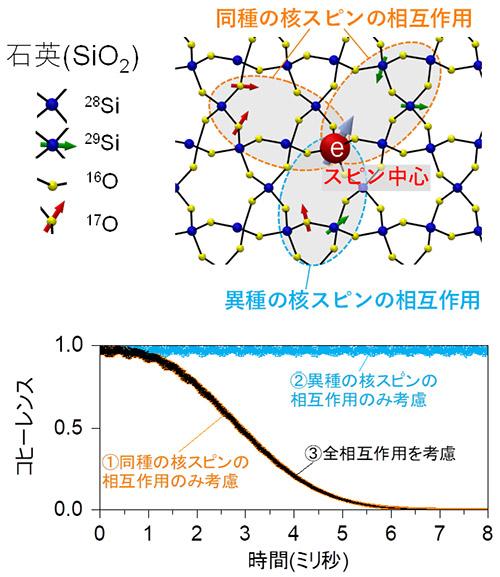
図2 異種核スピン浴のデカップリング (上)スピン中心周囲の核スピンからの相互作用のイメージ (下)各相互作用を加味した際のスピン量子状態(コヒーレンス)
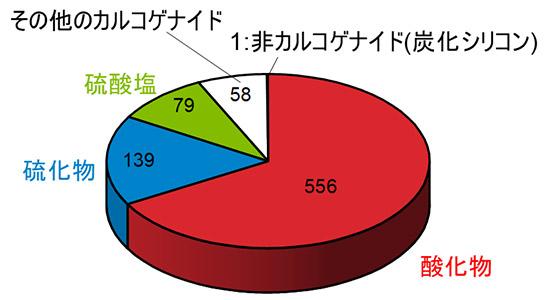
図3 スケーリング則を用いたT2予測の一例 天然存在比を持つ12,000物質について予測したT2のうち、1ミリ秒を超える約800物質の分類。
用語解説
- 注1) 固体中のスピン中心、ダイヤモンド窒素―空孔中心(NV中心)
- ダイヤモンドは炭素で構成されていますが、ある1つの炭素原子が1つの窒素原子で置き換わり、置き換わった窒素原子に隣接する1つの炭素原子にさらに欠損(空孔)が生じた部分を窒素―空孔中心(省略してNV中心)と呼びます。自然界でもまれに「ピンクダイヤモンド」として析出することがありますが、現在は欠陥を含まないダイヤモンドから効率的に作製する技術が確立されています。
このダイヤモンドNV中心は、(1)基底状態が三重項状態を取る(2)電子スピン緩和時間が長い(3)レーザー光により容易に量子状態を初期化可能 という量子ビット注3)として優れた性質を有しており、これまで最も精力的な研究が行われてきました。こうした単結晶中の原子レベルのごく微小な領域で原子配列が乱れた部分を点欠陥と呼びます。特にダイヤモンドNV中心のように点欠陥がスピン注3)の源となる場合には、これを固体中のスピン中心と呼び、着色の原因となる場合には色中心と呼ぶこともあります。
- 注2) 位相緩和時間
- ビット「0」と「1」の状態間に相互作用がある場合、各状態は完全には区別することができません。スピン中心の場合、この状態間、あるいは別の状態を介した相互作用のON/OFFをレーザー光や高周波磁場により高度に制御することで初期化や量子操作を行います。実際の材料では、これらの意図的に与える外場の他、結晶との熱的な相互作用、核スピンとの磁気的相互作用、結晶中の電荷による電気的相互作用などの意図しない相互作用が存在します。これらの相互作用は常に量子状態を混ぜるため、ビットの区別の精度を悪化させます。初期化してから状態が混ざるまでの時間を位相緩和時間と呼び、その時間は主にスピン中心を構成する母体材料で決定されます。位相緩和時間よりも長い時間では、上記ビットの判別可能性の問題により量子計算が不正確になるため、量子操作時間よりも十分に長い位相緩和時間が要求されます。
- 注3) 量子ビット、もつれ、量子コンピューター、スピン、電子スピン、核スピン、g因子
- ある物質のサイズを小さくしていくと、量子的性質が発現することがあります。例えば「スピン」と呼ばれる磁性の源の持つ量子的性質はナノメートル(10のマイナス9乗メートル)以下のスケールで顕著に見られ、微細加工技術の進展とともに様々な関連現象が発見されてきました。この量子的性質には古典物性とは異なる様々な特徴があります。その1つに「2つの量子状態を同時に取ることができる」という性質があります。
電子には、磁性の源となるスピンという性質があります。自由電子の場合には上向きと下向きの2つの状態を取ることができ、これがビットの「0」と「1」の状態に対応します。ハードディスクなどの磁性メモリでは、たくさんの自由電子スピンが揃っており、そのスピン方向が古典ビットと対応します。これらのデバイスでは、電子スピンが最低でも数万というオーダーで集まっており、量子的性質は見られません。一方で、孤立スピン中心のように単一か、それに近い数のスピンでは、スピンは上向きと下向きの状態両方を「同時に取る」ことができます。
全ての原子は原子核と電子により構成されます。原子核は中性子と陽子により構成されます。中性子と陽子はそれぞれスピンを持ちますが、この大きさは自由電子のスピンの大きさと比較して約1000分の1です。原子核全体としてのスピンは陽子や中性子のスピンが複雑に合成され、その大きさを表すのがg因子です。
量子ビットの2つのビット状態を「同時に取る」ことが可能な性質を利用し、2状態を重ね合わせた状態を同時に計算するのが量子計算や量子コンピューターです。量子コンピューターは古典コンピューターと比較して桁違いに高速に問題を解決することができる場合があることが示されています。例えば古典コンピューターが苦手とし、現代の暗号通信の基盤となっている素因数分解を高速に計算するアルゴリズムが開発されています。
- 注4) 量子ビットに適した固体中のスピン中心は?~ブレイクスルーへ向けた物性・材料の探索指針~
- 量子ビットとしての材料選択の幅を拡大するため、本研究チームは2021年4月に量子ビット材料選定に対する包括的ガイドラインを発表しました。(東北大学プレスリリース「量子ビットに適した固体中のスピン中心は?~ブレイクスルーへ向けた物性・材料の探索指針~
 」)
」)
- 注5) シュレーディンガー方程式、ハイゼンベルグ方程式
- 量子系の状態を表す波動関数と呼ばれる量がどのような状態をとり、どのように時間的に変化するのかを示す、量子力学の基本方程式がシュレーディンガー方程式と呼ばれます。これと等価な基本方程式として、ハイゼンベルグ方程式があり、こちらは密度行列と呼ばれる状態を表す行列を用いてシュレーディンガー方程式と同様に状態とその時間変化を記述します。
- 注6) 行列計算
- 表のように縦と横に配置した数のまとまりで、例えば\[\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}\]を大きさ2×2の行列と呼びます。行列には四則演算やその他の様々な演算を定義することができます。シュレーディンガー方程式やハイゼンベルグ方程式は行列により表すことができます。これらの方程式に基づいてT2を求めることができますので、T2は原理的には行列計算により求めることができます。一方で、本文で述べた通り、実際の材料の量子状態は21000×21000のような途方もなく巨大な行列で表され、そのままではT2計算は不可能です。
行列計算は機械学習をはじめとしたデータサイエンスにおいても中心的な役割を果たし、AI人材育成の観点から、平成29年度以降の最新の文部科学省の指導要領では、高等学校における数学Cの教材となっています。
- 注7) クラスター相関展開(CCE)
- 系全体の自由エネルギーを、系を構成する比較的小さなクラスターに分けて、それぞれの自由エネルギーと、その相互作用により記述する手法である、「クラスター展開」を、エコー計算に応用したものです。完全なハミルトニアンが含むN体相互作用の次数Nにより展開するため、次数の上限を決めることで計算を簡便化することが可能です。
例えば、系全体の完全な密度行列計算を行う際には、本文で述べた通り巨大なハミルトニアンの時間発展計算を行うための膨大なリソースが必要となりますが、ハーンエコーを支配する二体相互作用を加味するのであれば、二次のクラスター相関展開(CCE-2)を考慮すれば十分です。この際、一度に考慮するハミルトニアンのサイズは計算機で取り扱うには十分な大きさであり、こうした比較的小さなサイズの行列計算を多数回繰り返すことにより現実的な計算時間のハーンエコー計算が可能となりました。実際、2008年頃に発表されたハーンエコー信号のCCE計算による再現は、実験的に報告されたエコー信号を良く再現することが報告され、徐々にその有用性が評価されつつあります。2016年には、初めてSiCについてもT2が計算され、クラスター相関展開の有用性は最近認められつつあり、化合物においてもCCE計算を用いた現実的な時間でのT2計算・予測が可能となりました。
論文情報
| Title: |
“Generalized scaling of spin qubit coherence in over 12,000 host materials”
(1万2千を超える母体材料に於けるスピン量子ビットのコヒーレンスの一般化スケーリング) |
| Authors: |
Shun Kanai, F. Joseph Heremans, Hosung Seo, Gary Wolfowicz, Christopher P. Anderson, Sean E. Sullivan, Mykyta Onizhuk, Giulia Galli, David D. Awschalom, and Hideo Ohno |
| Journal: |
Proceedings of the National Academy of Sciences of the United States of America |
| DOI: |
10.1073/pnas.2121808119 |
問い合わせ先
研究に関すること
JST事業に関すること
報道に関すること





 」)
」)