

〜カーボンナノチューブとベルト状分子の接点は?〜
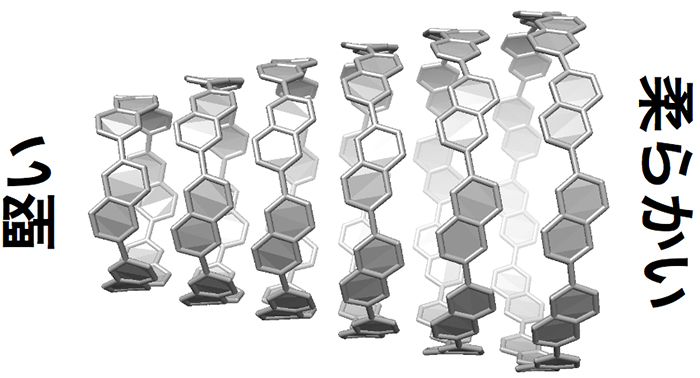 ナフタレンからつくった筒のような構造を持つベルト状分子の柔らかさ。「パネルの枚数を何枚にすれば,パネルが回転しない堅いカーボンナノチューブのような構造になるのか?」この根源的な問いについて数学と有機化学の組み合わせから答えが得られた。
ナフタレンからつくった筒のような構造を持つベルト状分子の柔らかさ。「パネルの枚数を何枚にすれば,パネルが回転しない堅いカーボンナノチューブのような構造になるのか?」この根源的な問いについて数学と有機化学の組み合わせから答えが得られた。
東北大学原子分子材料科学高等研究機構(AIMR)の磯部寛之主任研究者(JST ERATO磯部縮退π集積プロジェクト研究総括、東京大学大学院理学系研究科教授)と小谷元子機構長の共同研究グループは、ベルト状分子の持つ構造的特徴を化学的・幾何学的に明確にすることに成功しました。
現在、さまざまな分野での展開が期待されているカーボンナノチューブですが、長さ、太さ、あるいは炭素原子の並び方がさまざまなものの複雑な混合物であるために、化学物質(分子性物質)としての性質・特徴が明らかではありません。そのような中、カーボンナノチューブと同じ構造的要素を備えたモデル分子を生み出し、その特徴を明確にしようとする研究が世界的に注目されています。複数の芳香族分子を輪になるように結合することで構造が一義・明確なベルト状分子をつくりだし、その化学的性質を明らかにしようとする研究です。ベルト状分子自身が、これまでにない曲面を有した分子構造を持っていることから、未解明なことが多く、挑戦的な研究課題となっています。ベルト状分子は、芳香族分子をパネルのようにしてベルト(筒)を形づくりますが、そのパネル同士が単結合でつながっているために、芳香族分子がくるくると回転してしまう可能性があります。パネルが回転してしまうとカーボンナノチューブの「筒状の壁構造」を再現した構造になりません。しかし、実際にパネルが回転しているのかどうか、あるいは、何枚のパネルならばその回転を止められるのかという極めて基本的なことでさえわかっていませんでした。今回の研究では、まず、ナフタレンという芳香族分子をパネルにし、パネル数の異なる6種類のベルト状分子をつくりだしました。そして、そのパネルが回転する温度や、回転に必要なエネルギーという重要な基礎的性質を明らかにしました。また、6枚のナフタレンをベルト状分子とした際、室温でパネルが回転しない「堅い構造」が存在することが明らかとなりました。本研究のユニークな点は、構造的特徴を解き明かしたのが有機化学者と数学者との共同研究であったことです。「芳香族分子をパネルにしたベルト状分子では、何枚のパネルのときに何種類の異なる構造(異性体)が存在し得るのか」という最も根源的な問いに解答を与えたのが数学でした。この解答を基にして始めて「堅い(パネルが回転しない)」「柔らかい(パネルが回転する)」という化学的性質を明らかにできたものです。ベルト状分子の基本的性質が明らかになったことで、カーボンナノチューブの化学的特徴を明確にするための一歩が記されました。
本発表では、一般の方にもわかりやすくなるよう対話形式での解説を、内容説明に代えさせていただきます(以下は、内容説明のための仮想的な対話であり、実際の研究の進行とは必ずしも一致していません)。
| C博士(化学者): | カーボンナノチューブの一部分を切り出した筒のような構造を持つ「ベルト状分子」を有機化学的につくりだしました。ただ、その分子構造が複雑で、なかなかはっきりしたことが言えません。M博士、数学的に答えを出せたりしませんか? |
|---|---|
| M博士(数学者): | 数学で有機化学の問題が解けるでしょうか・・・。どんな問題ですか? |
| C博士: | 私たちの研究室では、芳香族分子といわれる平らな分子をパネルにして、その何枚かを一本の糸(結合)でつないで、まるめ、ベルト状にしています。パネルを数珠つなぎしたブレスレットのような格好といった方がわかりやすいかもしれないですが・・・。そうすると、カーボンナノチューブを模した筒のような構造が出来上がります(読者は表紙絵を参照のこと)。この筒のような構造が頑丈であればカーボンナノチューブの壁構造を再現した構造となります。今回、パネルの数が違うベルト状分子をいくつかシリーズでつくって、その筒のような構造が頑丈なのかどうかを調べました。ただ、そもそも、その分子構造の幾何学を理解するのに苦慮しています。 |
| M博士: | はあ。まだ、よくわかりませんが・・・。 |
| C博士: | 使ったパネル(芳香族分子)はナフタレンという、タンスの防虫剤などにも使われている分子なのですが、それをパネルにしてベルトをつくると、そこに表と裏という関係が生まれます。今回の場合、表と裏は鏡に映した関係にあります。 |
| M博士: | 表と裏・・・なんとなく数学的な感じになってきましたね。 |
| C博士: | パネルを6枚から11枚にした6種類のベルト状分子をつくったのですが、それぞれの分子に何種類の構造があるのかがわからないのです。6枚のパネルを使うと、表裏が6種類あるので全部で26通り、つまり64通りのベルトができます。ただ、ベルト状になっているので、64通りの中で表裏の並び順が同じとなっているものが出てくるんです。それから鏡に映してどうなるかということも考えなければならなくて・・・。鏡に映すと表は裏に、裏は表になるのですが、その鏡に映す操作をした後に重ならなくなるものの数も別に数えなければならないのです。 |
| M博士: | ややこしそうですが、まさに数学の問題のようですね。 |
| C博士: | 化学の世界では、表裏の並び順が別種となるものを立体異性体と呼びます。それぞれの立体異性体は異なる性質を持つので、物質を理解する上で、とても大事な区別です。そして、立体異性体を細かく区分けすると、さらに二種類あるんです。まず、並び順が異なるもの同士はジアステレオマーという関係となります。そのジアステレオマーの中でも鏡に映した構造が、もともとの構造とは重ならなくなってしまう性質を持つもの同士を、エナンチオマーと呼びます。ちょうど右手と左手のような関係です。それぞれ物質の性質を理解する上で、大切な特徴になっています。 |
| M博士: | 大まかには把握できました。それで知りたいことは、どのようなことでしょうか? |
| C博士: | n枚のパネルを使ったときの、立体異性体、ジアステレオマー、エナンチオマーの組、それぞれの数が知りたいのです。 |
| M博士: | なんとなく数学で解けそうな気がします。もう少し問題を整理するために、例えば、オセロのコマをパネルにしてみましょうか。白黒の二色が表裏だからわかりやすいでしょう。(写真1)一番単純な6枚パネルのベルトを、つくってみてください。 |
 写真1:オセロのコマ
写真1:オセロのコマ
| C博士: | オセロを使った場合には、鏡に映すと表が裏になるという点でちょっと混乱しそうですので、まずは「鏡に映す操作」というのを説明しておきます。 |
|---|---|
| M博士: | はい。お願いします。 |
| C博士: | 今回のナフタレンというパネルには表と裏があるのですが、オセロのパネルでは、それを白と黒で象徴して表すことになります。ちょうど、こんな感じです。(写真2) |
 写真2:「鏡像関係」を示すオセロのコマ
写真2:「鏡像関係」を示すオセロのコマ
図上部に示したナフタレンに表と裏があることを色で示すこととなる。
| M博士: | 実物では、右と左が鏡に映した関係になっているのですね。そして、鏡に映したら表裏が入れ替わることを、オセロでは白と黒の色の入れ替わりが示していると・・・。 |
|---|---|
| C博士: | そうです。化学では鏡像関係と言いますが、右のナフタレンと左のナフタレンは鏡に映した関係になっていて、それをオセロの白と黒が象徴的に表すことになります。お互いに重なり合わない関係になるときに、お互いがエナンチオマーの関係にあると理解されます。 |
| M博士: | 了解しました。 |
| C博士: | それでは、オセロ6枚を連ねてベルトをつくります。まずはジアステレオマーをつくります・・・できました。(写真3)それぞれのコマは接しているところが、1本の糸でつながっています。 |
 写真3:オセロのコマを6枚つかったベルト。ジアステレオマーは8種類。
写真3:オセロのコマを6枚つかったベルト。ジアステレオマーは8種類。
<>
| M博士: | 全部で8種類ですね。 |
|---|---|
| C博士: | はい。そして「鏡に映す操作」をすると、この8種類が2つの性質に大別できることがわかってきます。 |
| M博士: | やってみましょう。「鏡に映す」と表裏が入れ替わるので、色が入れ替わるのでしたね。 |
| C博士: | そうです。 |
| M博士: | ・・・できました。(写真4)どうでしょう。 |
 写真4:オセロのコマを6枚つかったベルト.左のボードと右のボードの中央に鏡を立てたと想定している.鏡に映ると白は黒に,黒は白に入れ替わり,右と左のボードの鏡像体がエナンチオマーと呼ばれる組となる。
写真4:オセロのコマを6枚つかったベルト.左のボードと右のボードの中央に鏡を立てたと想定している.鏡に映ると白は黒に,黒は白に入れ替わり,右と左のボードの鏡像体がエナンチオマーと呼ばれる組となる。
| C博士: | はい。そうですね。そして、前列の3つと中央・後列の5つは違う性質を持っていることが区別できることがおわかりでしょうか。例えば、左のボードの前列左端のベルトを鏡に映すと、右のボードの前列右端のベルトになりますが、この2つは実は全く同じものです。 |
|---|---|
| M博士: | 左のボードの前列左端のベルトのパネルを、手前から時計回りに外側の色を読むと「白・白・黒・黒・黒・白」です。右のボードの前列右端のベルトのパネルを同じように読むと「黒・黒・白・白・白・黒」ですが・・・読み始めの場所を変えて後ろの方から読むと「白・白・黒・黒・黒・白」。本当ですね。全く同じで重なります。前列中央のものはもう少し複雑そうですが・・・色を読んでいく方向は気に掛けないで良いのですよね? |
| C博士: | はい。順番がどうなっているかを確認するだけですので、パネルを回さなければベルト自体を回したりひっくり返したりして、重なるかどうかを考えれば良いことになります。その結果、前列の3つは「鏡に映しても変わらない性質」ということがわかります。(写真5)ところが中央列と後列は「鏡に映す操作」を行った結果、別のものになってしまいます。例えば左のボードの中央列左端のベルトのパネルは、手前から時計回りに外側の色を読むと「白・黒・白・白・白・黒」。 |
 写真5:オセロのコマを6枚つかったベルト. 前列の3つは「鏡に映す操作」を行っても,同じものとなる。
写真5:オセロのコマを6枚つかったベルト. 前列の3つは「鏡に映す操作」を行っても,同じものとなる。
| M博士: | 鏡に映したものは「黒・白・黒・黒・黒・白」です。本当ですね。重ならないようになっています。 |
|---|---|
| C博士: | 中央列と後列の5つは「鏡に映すと別のものになってしまう性質」なんです。(写真6)これがエナンチオマーの組です。 |
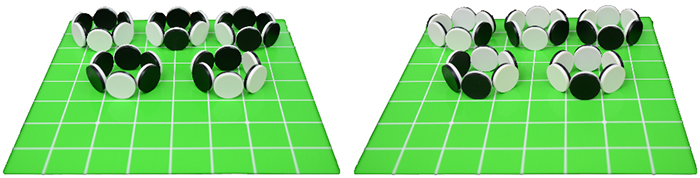 写真6:オセロのコマを6枚つかったベルト。 中央列と後列の5つは「鏡に映す操作」を行った結果、別のものとなる「エナンチオマーの組」。
写真6:オセロのコマを6枚つかったベルト。 中央列と後列の5つは「鏡に映す操作」を行った結果、別のものとなる「エナンチオマーの組」。
| M博士: | わかりました。ジアステレオマーの数は最初の8種類(写真3)。鏡に映した結果、右のボードの中央列・後列のものが、新しい種類「エナンチオマー」として5種類あらわれて(写真6)、立体異性体の総数はその和の13種類ということになるのですね。(写真7) |
|---|
 写真7:オセロのコマを6枚つかったベルト。13種類の立体異性体すべてを並べたもの。左のボードの一群がジアステレオマー(8種類)。右のボードの一群は、エナンチオマー(5種類)。
写真7:オセロのコマを6枚つかったベルト。13種類の立体異性体すべてを並べたもの。左のボードの一群がジアステレオマー(8種類)。右のボードの一群は、エナンチオマー(5種類)。
| C博士: | その通りです。立体異性体はそれぞれ性質が異なるので、その数と構造を知ることは化学の世界で、とても重要なこととなります。そして、エナンチオマー同士は立体異性体の中でも特別な関係で、基本的な性質が同じなのに、光の吸収の仕方など、対称性が関わった性質のみが違ってきます。 |
|---|---|
| M博士: | ・・・お役に立てそうです。この問題ならば、ちょっと複雑な式になりますが、数学で解けちゃいますよ。二色ネックレスという問題が知られているんです。これは数学で良く知られた「バーンサイドの定理」の応用です。高校数学で扱っている円順列の発展形ですね。まずは立体異性体の総数から行きましょうか。n枚のパネルをベルトにして、nが奇数の場合は、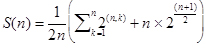 こんな式で数がだせます。数式の意味は高校数学の教科書に出ていますが、確認しておきますと(n,k)というのは、nとkの最大公約数という意味です。それからnが偶数だったら、 こんな式で数がだせます。数式の意味は高校数学の教科書に出ていますが、確認しておきますと(n,k)というのは、nとkの最大公約数という意味です。それからnが偶数だったら、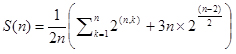 この式ですね。 この式ですね。 |
| C博士: | なんと・・・有機化学でも数学が使えるのですね・・・。 |
| M博士: | 続けますよ。nが奇数のときのジアステレオマーの数は、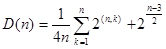 こうなります。そして、nが偶数ならこうです。 こうなります。そして、nが偶数ならこうです。 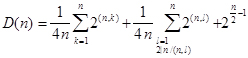 |
| C博士: | 素晴らしい、と言いたいところなのですが、最後の式の2|n/(n,l)というのはなんでしょうか? |
| M博士: | n/(n,l)のうち偶数のときの数だけを取り上げなさいという意味ですね。 |
| C博士: | ・・・これでなんとか数を出せそうな気がします。 |
| M博士: | エナンチオマーの組の数も数式が立てられますが、立体異性体の総数からジアステレオマーの数を引き算するのが、単純で簡単ですね。ちなみにこれらの式を使って出した数が正しいかどうか、確認できるデータベースもあります。 |
| C博士: | えっ・・・ |
| M博士: | オンライン整数列大辞典(OEIS;https://oeis.org/ )という数列に関するデータベースで、立体異性体はA000029、ジアステレオマーはA000011、エナンチオマーはA007147に答えがあります。 )という数列に関するデータベースで、立体異性体はA000029、ジアステレオマーはA000011、エナンチオマーはA007147に答えがあります。 |
| C博士: | ・・・11枚だと2048通りの可能性の中から、立体異性体を126種類、ジアステレオマーとエナンチオマーを、それぞれ63種類も探し出さなければならなかったのですね。これでは、さすがに探し切れなかった・・・。 |
| M博士: | それでこの異性体の数から、どのようなことがわかるのですか? |
| C博士: | 細かいことは省いてしまいますが、ざっくり言いますとベルト状の構造が頑丈かどうかを調べるための基本情報として使います。測定したスペクトルが、いずれかの構造に対応しているのか、あるいは全ての構造の平均としてでてきたものなのか、を考えます。ところが、そもそもその考察で想定した構造が、全ての構造を網羅していたのかどうかでさえわからなかったんです。教えていただいた異性体数からすると、全ての実験データが揃っているようです。つまり、その答えがでたということになります。 |
| M博士: | どんな? |
| C博士: | 先ほどのオセロのベルトですが、一本の糸だけでつないでいるので、パネルがくるくる回ってしまいますよね? |
| M博士: | そうですね。パネルが回っていると、こんなふうに傾いて筒の形からずれてしまうことがありますね。(写真8) |
 写真8:パネルの傾きにより筒のような構造ではなくなる。
写真8:パネルの傾きにより筒のような構造ではなくなる。
| C博士: | その通りです。カーボンナノチューブのモデルとして設計しているので、このパネルを回さないようにして筒の形を保つのが重要なのですが、どうすればパネルの回転が止まるのかを示す一般的な解が世の中にはありませんでした。パネルの数を少なくすれば、回転が遅くなるだろうという予想程度はあったのですが・・・。 |
|---|---|
| M博士: | 構造の根本的なことがわかっていなかったということですね。 |
| C博士: | そうなんです。その最も根本的なデータが、この研究で得られました。パネルの数と温度で構造の柔らかさがどう変わるかを調べたのです。その結果をまとめたものが図1です。 |
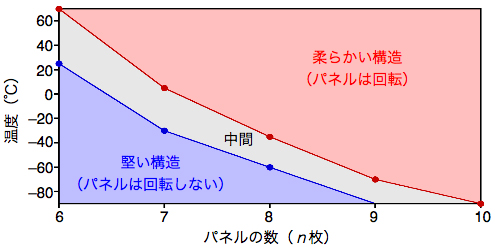 図1.パネルの数とベルト状構造の柔軟性。
図1.パネルの数とベルト状構造の柔軟性。
| M博士: | パネルの枚数が増えるとパネルは回りやすくなって、あるパネル枚数で、どの温度から回転し始めるのかということが示されているのですね。 |
|---|---|
| C博士: | そうです。漠然とした予想はありましたが、この研究で初めて、パネルの回転が始まる温度や、回転させるために必要なエネルギーといった重要な性質を定量化できました。定量化した値が、筒のような構造を理解するための基礎データとなるからです。このデータの中で、もう1つ重要なことは、パネルが6枚の場合、20 ℃程度の室温では堅い筒のような構造が存在していたことです。つまり、ナフタレンをパネルとしたベルト状分子の場合、パネル6枚以下からカーボンナノチューブの円筒状の壁を模した構造を持つということがわかりました。 |
| M博士: | そうなのですね。ちなみに堅い構造のときに筒のような構造になっているというのは、確かなのですか? |
| C博士: | はい。まずはスペクトル分析でわかっています。それから、パネルが7枚の場合にはX線回折による単結晶構造解析という分析方法で、–178 °Cでの分子の形を見ています。その分子構造が図2です。 |
 図2.パネル7枚のベルト状分子の分子構造。単結晶構造解析から得られた実験データ。数値はカーボンナノチューブとしての構造様式を示している。
図2.パネル7枚のベルト状分子の分子構造。単結晶構造解析から得られた実験データ。数値はカーボンナノチューブとしての構造様式を示している。
| M博士: | あ、本当ですね。確かに筒みたいになっています。 |
|---|---|
| C博士: | 今回の研究で、筒のような構造を保つにはどうすれば良いのかを理解するために最も基本となるデータが得られました。将来、こうした筒のような構造をさらに調べていくと、カーボンナノチューブの性質を深く理解できるのではないかと期待しています。 |
| M博士: | これからが楽しみですね。 |
今回の研究は、有機化学と数学を組み合わせることで、根本的な問題に解がもたらされたものです。数学者にとっては、非常に初歩的な問題であっても、化学の世界で使うことで、その研究最前線で理解されていなかったことが、わかるようになることを示す好例といえます。
この研究が受けた主な支援は以下の通りです:
・JST戦略的創造研究推進事業総括実施型研究(ERATO)「磯部縮退π集積プロジェクト
・世界トップレベル研究拠点プログラム(WPI)
・科学研究費助成事業
また、X線回折による分子構造決定には、一部、高エネルギー加速器研究機構(KEK)フォトンファクトリー(PF-AR NE3A)の最先端設備が活用されています。
研究成果は、国際学術雑誌「米国科学アカデミー紀要(PNAS; Proceedings of National Academy of Science, U.S.A.)に2016年6月27日の週に掲載されます。
研究者の氏名・所属:
| 孫 哲 (そん てつ) |
ERATO磯部縮退π集積プロジェクト 研究員 東北大学原子分子材料科学高等研究機構(AIMR) 助教 |
|---|---|
| 末永 拓也 (すえなが たくや) |
東北大学大学院理学研究科 大学院生 |
| サルカール パランタップ | 東北大学原子分子材料科学高等研究機構(AIMR) 助手 |
| 佐藤 宗太 (さとう そうた) |
ERATO磯部縮退π集積プロジェクト グループリーダー 東北大学原子分子材料科学高等研究機構(AIMR) 准教授 |
| 小谷 元子 (こたに もとこ) |
東北大学原子分子材料科学高等研究機構(AIMR) 機構長 |
| 磯部 寛之 (いそべ ひろゆき) |
東京大学大学院理学系研究科 教授 ERATO磯部縮退π集積プロジェクト 研究総括 東北大学原子分子材料科学高等研究機構(AIMR) 主任研究者 |
米国科学アカデミー紀要(PNAS)
論文名:Stereoisomerism, crystal structures, and dynamics of belt-shaped cyclonaphthylenes
(和文:ベルト状分子シクロナフチレンの立体異性、結晶構造と動的挙動)
DOI: 10.1073/pnas.1606530113 )
)
磯部寛之教授らの代表的な関連先行研究については、以下のプレスリリースもご参照いただけます:



磯部 寛之
東北大学原子分子材料科学高等研究機構(AIMR) 主任研究者
| TEL/FAX : | 022-217-6160(東北大)・03-5841-4162(東大)/022-795-6233 |
|---|---|
| E-MAIL : | isobe@m.tohoku.ac.jp |
| Lab HP : | http://www.jst.go.jp/erato/isobe/ |
佐藤 宗太
東北大学原子分子材料科学高等研究機構 准教授
| TEL : | 022-217-6160 |
|---|---|
| E-MAIL : | satosota@m.tohoku.ac.jp |
JST事業に関すること
大山 健志(オオヤマ タケシ)
科学技術振興機構研究プロジェクト推進部
| TEL/FAX : | 03-3512-3528/03-3222-2068 |
|---|---|
| E-MAIL : | eratowww@jst.go.jp |
報道担当
東北大学原子分子材料科学高等研究機構(AIMR)
広報・アウトリーチオフィス
| TEL : | 022-217-6146 |
|---|---|
| E-MAIL : | aimr-outreach@grp.tohoku.ac.jp |
科学技術振興機構広報課
| TEL/FAX : | 03-5214-8404/03-5214-8432 |
|---|---|
| E-MAIL : | jstkoho@jst.go.jp |
東京大学大学院理学系研究科・理学部広報室
| TEL : | 03-5841-0654 |
|---|---|
| E-MAIL : | kouhou@adm.s.u-tokyo.ac.jp |