

-材料科学と数学とのコラボ-
東北大学原子分子材料科学高等研究機構(AIMR)の柳沼晋助教、中島千尋助教、中山幸仁准教授らの研究グループは、ガスアトマイズ法(※1)により作製されたアモルファス合金の粉体とワイヤーを含む生成物の直径分布が対数正規分布に従うことを見出しました。これにより、生成したワイヤー形状のサイズ評価が初めて可能となりました。この評価基準をベースに、材料が糸状になる曳糸性と流体の不安定性との関連から導き出された無次元数を用いて、粉体とワイヤーの生成条件が見出されました。今回の研究成果は、サイズが揃ったナノワイヤー(※2)の作製手法に繋がることが期待でき、ナノテクノロジー研究におけるナノワイヤーの産業への応用に大きく道を開くものです。
本研究成果は、ネイチャー出版グループのScientific Reports誌に平成27年6月1日(英国時間)に掲載されます。
対数正規分布は、身近な生活によく現れる自然現象や社会現象に頻繁に出てくる統計分布の一種として知られています。例えば、宇宙にある銀河の個数密度、ガラスの破壊現象、人の咀嚼による破片のサイズ、児童の身長や体重、研究者の論文発表数、比例代表選挙の得票数、株価の収益率、年収所得の分布など多岐に渡っており、様々な現象を解析するために用いられています。
これまでに我々はガスアトマイズ法を用いて、アモルファス合金ナノワイヤーを低コストで大量生産できる手法を開発してきましたが、生成したナノワイヤーのサイズ分布を調べる評価法はなく、更にナノワイヤー化する際に粉体が混入してしまう問題を抱えていました。また、従来の粉末冶金の研究分野では、粉末状の生成物に対して対数正規分布関数を適合させて解析が進められてきましたが、ワイヤー形状に対して行われた例はありませんでした。溶融状態の合金は、高い粘性を持つため、これが引き延ばされると糸状になり易い性質(曳糸性)が発現されます。この曵糸現象は自然界でも見られ、ペレー(ハワイ島の火山の女神)の毛と呼ばれる火山噴出物は、高い粘性を持つマグマが噴気で引き伸ばされ髪の毛のように固まったものとして知られています。この曳糸性は、溶融した合金の粘性、表面張力、ならびに引き延ばし速度から評価することが可能ですが、更に生成されたワイヤー直径の評価基準が確立されれば、これをベースとして解析する手段が得られ、更に詳細なナノワイヤーの生成メカニズムの解明にも役立つことが期待できます。これによりサイズの揃ったナノワイヤーを生産するような研究も展開でき、産業的に利用できる可能性が拡がります。
今回、東北大学の研究グループは、パラジウム系アモルファス合金に対してガスアトマイズ法を用いて実験を行い、合金の溶湯温度を変化させた際に生成する形状や直径の分布を詳細に求めました(図1)。特にワイヤー形状の直径分布が対数正規分布に従うことを見出しました(図2)。これにより平均(※3)と標準偏差(※4)が求められ、これらの値を累積分布関数(※5)へ代入して、ワイヤー積算数の50%に相当する値、即ち中央値(※6)(メディアン径)が求められました(図3)。実験的にメディアン径が求められると、生成したワイヤーの評価基準が得られ、ワイヤーの形成機構について調べることが可能になります。
曳糸性とレイリー・プラトーの不安定性(※7)から、液糸と液滴の緩和時間の比がオーネゾルゲ数(※8)(Oh)と呼ばれる次元を持たない物理量として表すことができます。液糸の緩和時間が液滴の緩和時間よりも長い場合、即ちOh > 1の場合はワイヤー形状が優先的になり、反対に液滴の緩和時間が液糸の緩和時間よりも長くなる場合、即ちOh < 1の場合は粉末形状が優先的になります。今回の実験では、Ohが増加することによりワイヤー形状の比率も増加することが明らかになる一方で、ワイヤーの直径も増大することが判明しました(図4)。更に、Oh = 1近傍は細いナノワイヤーが主要生成物となるための最適条件であることが判明しました。
今後は粘性や表面張力の異なるアモルファス合金材料を用いて実験を行い、生成物が対数正規分布に則るかどうか検証するとともに、直径分布領域が狭くよりサイズの揃ったナノワイヤーの作製法の開発に繋がるよう研究を進める予定です。このサイズが揃ったナノワイヤーは産業的に、極小型磁気センサ、高機能性触媒材料、複合強化材料、透明導電膜などへの応用が期待できます。
本研究成果は、東北大学原子分子材料科学高等研究機構の柳沼晋助教(現 国立高等専門学校機構長野工業高等専門学校講師)、中島千尋助教、金子直人研究員、東北大学金属材料研究所の横山嘉彦准教授、東北大学原子分子材料科学高等研究機構の中山幸仁准教授との共同研究によるものです。また本研究の一部は、日本学術振興会(基盤研究B(25286019、代表:中山幸仁))、(若手研究B(26870058、代表:柳沼晋))、独立行政法人科学技術振興機構(A-STEP(H25 仙台II-463、代表:中山幸仁))、ならびにWPI-AIMR融合研究より研究助成を受けて実施されました。
 図1
図1
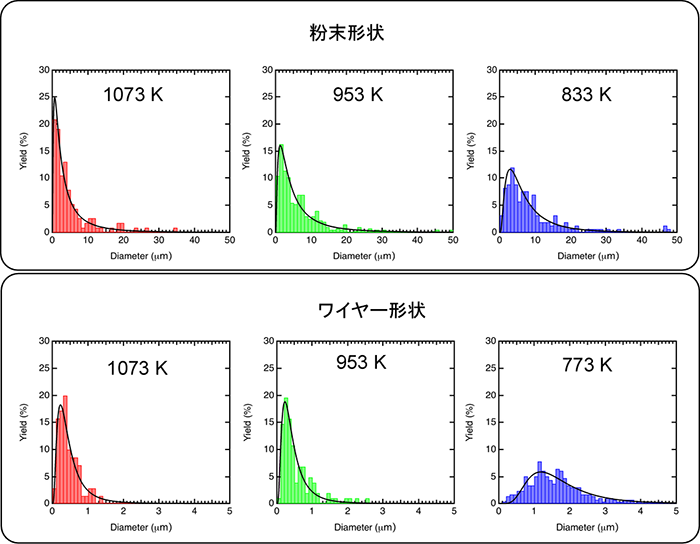 図2
図2
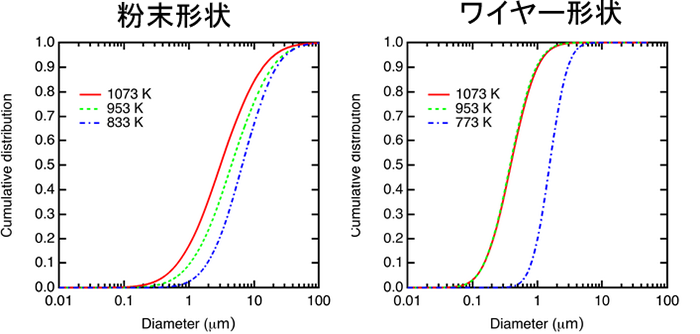 図3
図3
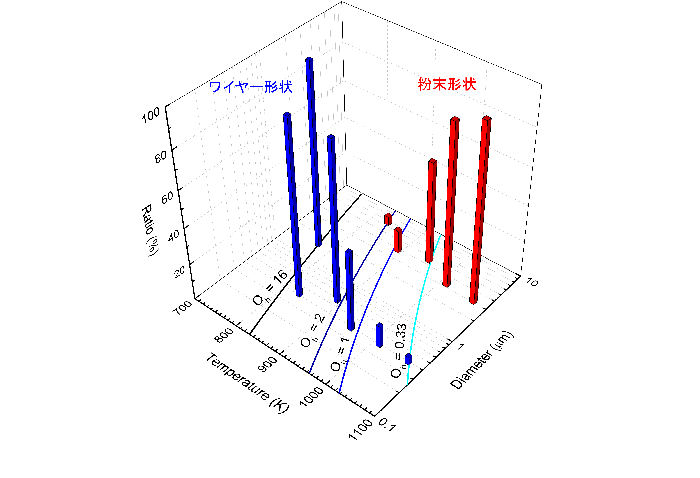 図4
図4
雑誌名:Scientific Reports
タイトル: Log-normal diameter distribution of Pd-based metallic glass droplet and wire
著者: S. Yaginuma, C. Nakajima, N. Kaneko, Y. Yokoyama, and K. S. Nakayama
研究に関すること
中山幸仁 (ナカヤマ コウジ)
東北大学原子分子材料科学高等研究機構(AIMR)准教授
| TEL : | 022-217-5950 |
|---|---|
| E-mail : | kojisn@wpi-aimr.tohoku.ac.jp |
報道に関すること
東北大学原子分子材料科学高等研究機構(AIMR) 広報・アウトリーチオフィス
| TEL : | 022-217-6146 |
|---|---|
| E-mail : | outreach@wpi-aimr.tohoku.ac.jp |