

08/29/2016
Reproduced, with permission, from Ref. 1 © 2016 Y. Hiraoka et al.
By harnessing the power of an emerging mathematical technique known as persistent homology, AIMR researchers have extracted important geometric information about the atomic configuration of the mostly random structure of glasses1.
Glasses range from window glass made from silica to metallic glasses. In contrast to the periodic atomic order of crystals, the atoms in glasses are largely randomly distributed. But glasses do not have entirely random structures, and their local atomic order can strongly influence their properties. However, characterizing this atomic order in glasses has proved very challenging because the order is largely masked by the overall randomness of glass structure.
Yasuaki Hiraoka of the AIMR at Tohoku University and his co-workers turned to applied mathematics for help. In particular, they explored a recently developed mathematical technique called persistent homology. This powerful analytical method can characterize geometric structures that lie hidden in large sets of data, and it is being applied in a wide range of fields.
“We used persistent homology to investigate one such geometric structure, namely the hierarchical relationship of rings in the atomic configuration of glasses,” explains Hiraoka.
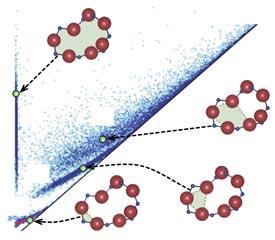
Employing a model of the atomic positions of a glass as the input, the researchers used software based on persistent homology to generate a graphical representation of the structure, which is known as a persistence diagram.
The persistence diagram reveals the presence of local multiscale structures in a material. Depending on geometrical parameters such as the size of the atoms and the distances between them, different ring-like configurations of atoms exist. For a perfectly random structure, no local ring structure is favored and the data background looks uniform. For a crystalline structure, geometric features are preferred and clear structures appear in the analysis. In the case of the silica glass studied, the results are intermediate between these two extremes: a uniform random-like background is observed along with the presence of a few ring-like structures, which are characterized by curves in the persistence diagram (see image).
This ability of persistent homology to uncover hierarchical structures that are hidden to conventional techniques is a powerful demonstration of the potential of this method for studying the structure and properties of glasses and other amorphous materials.
For the future, the team has set its sights even higher. “Our next target for amorphous structural analysis is to try to mathematically characterize the glass transition — one of the most important problems in current condensed-matter physics,” says Hiraoka.
This research highlight has been approved by the authors of the original article and all information and data contained within has been provided by said authors.