

Kelvin’s Conjecture and Experiments of Soap Films
奈良 知惠 研究推進員
(明治大学先端数理科学インスティテュート)
2016年12月16日(金) 14:30-15:30
AIMR本館2階 セミナー室
How can space be divided into cells of equal volume so as to minimize the (average) surface area of the boundary? In 1887, Lord Kelvin (William Thomson) conjectured that the partition made by a packing of congruent copies of the truncated octahedron with slightly curved faces is the solution (see Figure 1). His conjecture is based on the rules of Plateau (1873) in the theory of foams (see Figure 2). In1994, Denis Weaire, an Irish physicist, and Robert Phelan showed a counterexample to Kelvin’s conjecture, in which packing consists of two kinds of cells with curved faces.
If we restrict cells to space-fillers, congruent polyhedral tiles, we get the orthic version of Kelvin’s conjecture; the truncated octahedron has the minimum surface area among all polyhedral space-fillers. This conjecture is still open. In this paper we introduce the notion of doubly-covered polyhedra and their unfoldings, which leads to an approach for a partial solution of the new Kelvin’s conjecture.
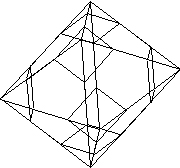 |
 |
|
| Figure 1. A truncated tetrahedron | Figure 2. Soap films obtained by a rectangular parallelepiped frame |
AIMR国際推進係
| 住所 : | 〒980-8577 仙台市青葉区片平2-1-1 |
|---|---|
| TEL : | 022-217-5971 |
| E-MAIL : | iac@grp.tohoku.ac.jp |