WPI-AIMR Math Unit

　▼Research Subjects 　▼Members 　▼Press Releases 　▼Seminar & Workshop 　▼Past Activities 　▼News & Informations 　▼Access & Contact 　▼Links

Research Subjects

A Mathematical Challenge to New Phase of Material Sciences
Collision of particle patterns in dissipative systems
Active Matter

----------------------------------

A Mathematical Challenge to New Phase
of Material Sciences

　The development of high-performance materials serves the well-being of human-society. Now that we observe and design nano-scale systems for the material development, demands for a new mathematical theory to describe nano-scale phenomena are increasing. By a mutually beneficial partnership between mathematics and material science, our research project aims to meet these demands and to develop mathematical models. This would enable us to design new compounds and to yield prescribed functional properties. The key, we believe, lies in the fundamental understanding of micro-meso-macroscopic structural relations and in the identification of mechanisms in terms of mathematics. In the future, this research team is expected to evolve into the research core of "mathematical materials sciences" with high integration of mathematical science, information science, physical chemistry and chemical physics, and materials science.

Main Research Subjects:

1. Design of K4 Lattice (Sunada Lattice) Characteristics and Its Synthesis
2. Development of Structured Illumination
3. Analysis of Ultrafast Phase Separation Dynamics
4. Achievement of High Heat-Conductivity in Heat-Resistant Polymers

▲TOP

-------------------------------------

Collision of particle patterns in dissipative systems

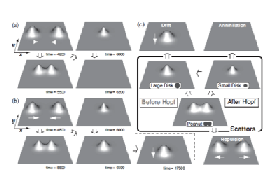
　Particle patterns mean any spatially localized structures sustained by the balance between inflow and outflow of energy/material which arise in the form of chemical blob, discharge pattern, morphological spot, and binary convection cell. These are modeled by typically three-component reaction diffusion systems or a couple of complex GL equations with concentration field. Strong interaction such as collision among particle patterns is a big challenge, since dissipative systems do not have many conservative quantities. Unlike weak-interaction through tails of those objects, there are so far no systematic methods to handle them because of large deformation of patterns during the collision process. We present a new approach to clarify a backbone structure behind the complicated transient collision process. A key ingredient lies in a hidden network of unstable solutions called scattors which play a a crucial role to understand the input-output relation for collision process (namely the relation of two dynamics before and after collision). More precisely, the associated network of scattors via heteroclinic connections forms a backbone for the whole collisional dynamics. It should be noted that collision dynamics for traveling breathers depends the phase differnce of those waves (see [3]). The viewpoint of scattor network seems quite useful for a large class of model systems arising in gas-discharge phenomena, chemical blobs, and binary fluid convection.

Relevant reference from our group:

[1] Y. Nishiura, T. Teramoto and K.-I. Ueda: "Scattering and separators in dissipative systems", Phys. Rev. E, 67: 056210 (2003)

[2] Y. Nishiura, T. Teramoto and K.-I. Ueda: "Dynamic transitions through scattors in dissipative systems", Chaos, 13(3): 962-972 (2003)

[3] T. Teramoto, K.-I. Ueda and Y. Nishiura: "Phase-dependent output of scattering process for traveling breathers", Phys. Rev. E, 69(4): 056224 (2004)

[4] Y. Nishiura, T. Teramoto and K.-I. Ueda: "Scattering of traveling spots in dissipative systems",
Chaos, 15: 047509-047519 (2005)

[5] T. Teramoto, K.-I. Ueda and Y. Nishiura: "Breathing Scattors in Dissipative Systems", Progress of Theoretical Physics Supplement No.161(2006)pp364-pp367.

▲TOP

-------------------------------------

Active Matter

　The statistical mechanics of "active" soft condensed materials have been attracting attention in last decades. The importance of this field is that such systems are closely related to biological phenomena, which give us unlimited imagination and intuition. In addition, they are found in most of industrial products sustaining our comfortable lives.
　Biological systems consume energy and exhibit their functions. Among the variety of phenomena, we are particularly interested in cell motility. Interestingly, cells can move without any external force. This is achieved by active force (stress) generation using energy of ATP. The goal of my study is to understand the general theory of self-propulsion particularly focusing on its mechanical aspects. As a first step, we are now investigating theoretical model of chemical systems in which particles and drops move spontaneously.

References:

[1] Natsuhiko Yoshinaga, Ken H. Nagai, Yutaka Sumino, Hiroyuki Kitahata: "Drift instability in the motion of a droplet with a reactive surface", http://arxiv.org/abs/1206.3625

[2] Hiroyuki Kitahata, Natsuhiko Yoshinaga, Ken H. Nagai, and Yutaka Sumino: "Spontaneous motion of a droplet coupled with a chemical wave", Physical Review E Rapid Communication, 84, 015101(R) (2011)

[3] Natsuhiko Yoshinaga and Philippe Marcq: "Contraction of cross-linked actomyosin bundles", to appear in Physical Biology (arXiv:1206.1746)

[4] Hong-Ren Jiang, Natsuhiko Yoshinaga, and Masaki Sano: "Active Motion of Janus Particle by Self-thermophoresis in Defocused Laser Beam", Physical Review Letters, 105, 268302 (2010)

[5] http://www.wpi-aimr.tohoku.ac.jp/~yoshinaga/index.html

▲TOP

-------------------------------------

【Latest News】

AIMR Math Group Seminar

Date: May. 29th (Thu) 2025
Speaker:

1. Dr. Naoki Sakata

2. Dr. Xiao Dongyuan

Advanced Institute for Materials Research Tohoku University｜Mathematical Science Group

▼Research Subjects ▼Members ▼Press Releases ▼Seminar & Workshop ▼Past Activities ▼News & Informations ▼Access & Contact ▼Links

Research Subjects

A Mathematical Challenge to New Phase of Material Sciences

Collision of particle patterns in dissipative systems

Active Matter

【Latest News】

　▼Research Subjects 　▼Members 　▼Press Releases 　▼Seminar & Workshop 　▼Past Activities 　▼News & Informations 　▼Access & Contact 　▼Links

A Mathematical Challenge to New Phase
of Material Sciences