研究
- Frustrated phases of block copolymers confined in nanospace and spontaneous morphological change via annealing
- Collision of spatially localized patterns
- Propagation in heterogeneous media
- Pulse generators
- Stability of singularly perturbed solutions -the SLEP method –
- Response of BZ waves to local pulse irradiation
- Multistate network model for pathfinding problems
- Topological approach to materials science
- Decision making via interaction with environments
- Self-replication, spatio-temporal chaos, and propagation failure
- Patterns on a growing domain
- Inhibitory or repulsively coupled oscillators
1. Frustrated phases of block copolymers confined in nanospace and spontaneous morphological change via annealing
We numerically study a set of coupled Cahn–Hilliard equations as a means to find morphologies of diblock copolymers in three-dimensional spherical confinement, which is a gradient of the free energy shown below. This approach allows us to find a variety of energy minimizers including rings, tennis balls, Janus balls and multipods among several others. Phase diagrams of confined morphologies are presented. We modify the size of the interface between microphases to control the number of holes in multipod morphologies. Comparison to experimental observation by transmission electron microtomography of multipods in polystyrene–polyisoprene diblock copolymers is also presented.
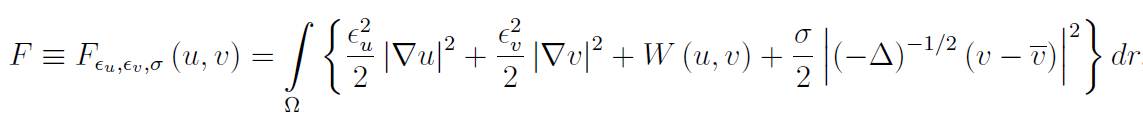
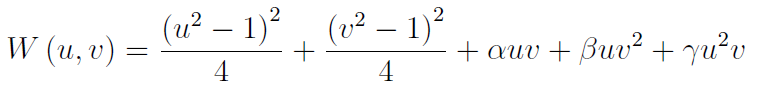

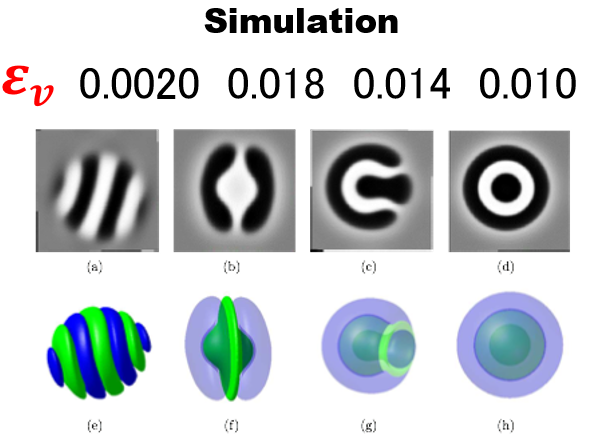
Annealing of block copolymers has become a tool of great importance to reconfigure nanoparticles. Herein, we present experimental results of annealing block copolymer nanoparticles and a theoretical model to describe the morphological transformation from ellipsoids with striped lamellae into onion-like spheres. A good correspondence between experimental findings and predictions of the model is observed. The model based on finding the steepest direction of descent of an appropriate free energy leads to a set of Cahn-Hilliard equations that correctly describes the dynamical transformation from striped ellipsoids into onion-like spheres and reverse onion-like particles, regardless of the nature of the annealing process. This universality makes possible to describe a variety of experimental conditions involving nanoparticles underlying a heating process. A notable advantage of the proposed approach is that it makes possible to selectively control the interaction between the confined block copolymer and the surrounding medium.
This feature endows the model with great versatility to reproduce several combined effects of surfactants in diverse conditions, including cases with reverse affinities for the block copolymer segments. A phase diagram to describe a variety of morphologies is presented. We employ relations between the temperature-dependent Flory-Huggins parameter and the width of the interfaces to account for changes in temperature due to the heating process.
Simulation results correctly show how the transformation evolves as the temperature increases. This increment in temperature corresponds to progressively smaller values of the interfacial width. We anticipate that the proposed approach will facilitate the design and a more precise control of experiments involving various kinds of annealing processes.

REFERENCE
- Edgar Avalos, Takeshi Higuchi, Takashi Teramoto, Hiroshi Yabu and Yasumasa Nishiura:“Frustrated phases under three-dimensional confinement simulated by a set of coupled Cahn–Hilliard equations”, Soft Matter, Issue 27, 2016, 12 : 5905–5914(2016)DOI: 10.1039/C6SM00429F
- Edgar Avalos, Takashi Teramoto, Hideaki Komiyama, Hiroshi Yabu and Yasumasa Nishiura: “Transformation of block copolymer nanoparticles from ellipsoids with striped lamellae into onion-like spheres and dynamical control via coupled CahnHilliard equations” (DOI:10.1021/acsomega.7b01557) ACS Omega (2018)
2. Collision of spatially localized patterns
a) Collision of localized patterns in dissipative systems
Strong interaction like collisions among localized patterns is one of the unexplored fields in nonlinear dynamics. In what follows I will describe it very briefly. Spatially localized dissipative structures are ubiquitous such as vortex, chemical blob, discharge patterns, granular patterns, and binary convective motion. When they are moving, it is unavoidable to observe various types of collisions. One of the main questions for the collision dynamics is that how we can describe the large deformation of each localized object at collision and predict its output. The strong collision usually causes topological changes such as merging into one body or splitting into several parts as well as annihilation. It is in general quite difficult to trace the details of the deformation unless it is a very weak interaction. We need a change in our way of thinking to solve this issue. So far we may stick too much to the deformation of each localized pattern and become shrouded in mystery. We try to characterize the hidden mechanism behind the deformation process. It may be instructive to think about the following metaphor: the droplet falling down the landscape with valleys and ridges. The motion of droplets on a rugged landscape is rather complicated; two droplets merge or split at the saddle points and they may sink into the underground, i.e., annihilation. On the other hand, the profile of the landscape remains unchanged and in fact it controls the behaviors of droplets. It may be worth to describe the landscape itself rather than complex deformation, namely to find where is a ridge or a valley, and how they are combined to form a whole landscape. Such a change of viewpoint has been proposed recently claiming that the network of unstable patterns relevant to the collision process constitutes the backbone structure of the deformation process, namely the deformation is guided by the connecting orbits among the nodes of the network. Each node is typically an unstable ordered pattern such as steady state or time-periodic solution. This view point is quite useful and can be applicable to various problems, especially, the dynamics in heterogeneous media is one of the interesting applications. External environments can be regarded as a heterogeneity for moving objects so that questions of adaptability in biological systems may fall in this category when they are reformulated in an appropriate way. See the recent works for more details.
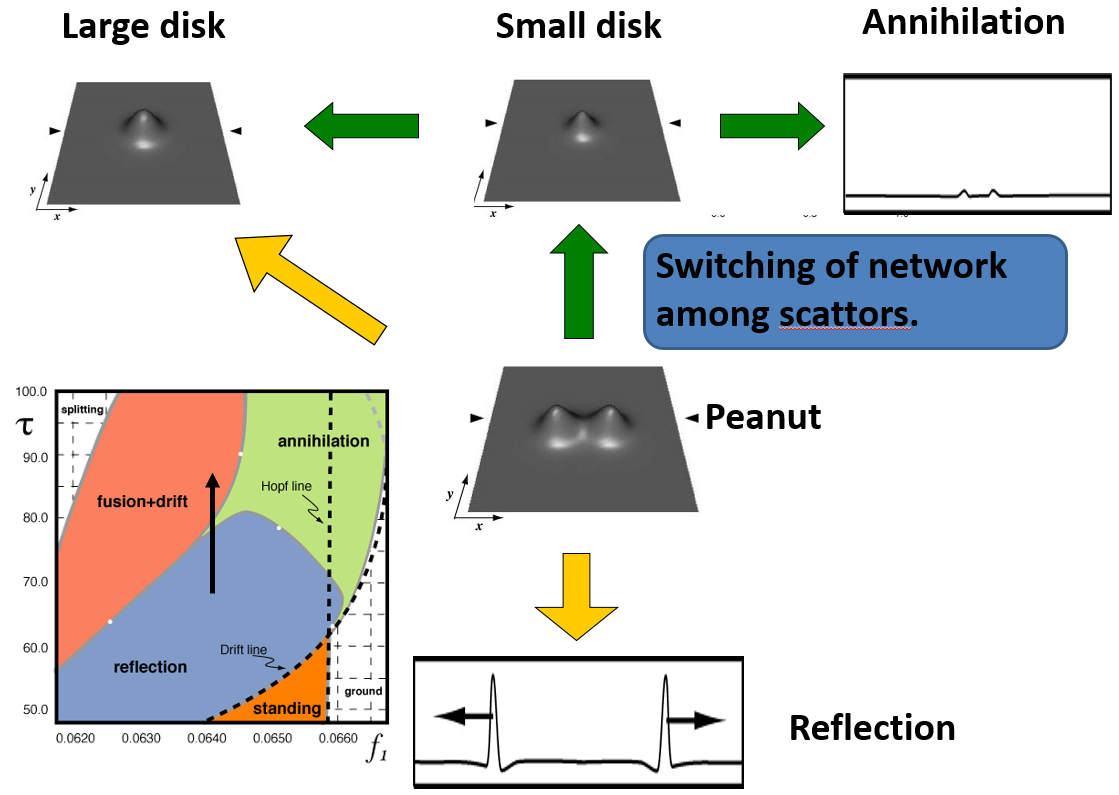
Particle patterns mean any spatially localized structures sustained by the balance between inflow and outflow of energy/material which arise in the form of chemical blob, discharge pattern, morphological spot, and binary convection cell. These are modeled by reaction diffusion systems, complex GL equations, the Navier-Stokes equations coupled with temperature and concentration fields. Strong interaction such as collisions among particle patterns is a big challenge, since large deformation is usually associated with the event, and input-output relation is quite complicated. Unlike weak-interaction through the tails of those objects, there are so far no systematic methods to describe the dynamic process of collisions. We present a new approach to clarify a backbone structure behind the complicated transient collision process. A key ingredient lies in a hidden network of unstable solutions called scattors which play a crucial role to understand the input-output relation for collision process (namely the relation of two dynamics before and after collision). More precisely, the associated network of scattors via heteroclinic connections forms a backbone for the whole collisional dynamics. The viewpoint of scattor network seems quite useful for a large class of model systems arising in gas-discharge phenomena, chemical blobs, and binary fluid convection.
REFERENCE
- Y. Nishiura, T. Teramoto and K.-I. Ueda: “Scattering and separators in dissipative systems“, Phys. Rev. E, 67: 056210 (2003)
- Y. Nishiura, T. Teramoto and K.-I. Ueda: “Dynamic transitions through scattors in dissipative systems“, Chaos, 13(3): 962-972 (2003)
- T. Teramoto, K.-I. Ueda and Y. Nishiura: “Phase-dependent output of scattering process for traveling breathers“, Phys. Rev. E, 69(4): 056224 (2004)
- Y. Nishiura, T. Teramoto and K.-I. Ueda: “Scattering of traveling spots in dissipative systems“, Chaos, 15: 047509-047519 (2005)
- T. Teramoto, K.-I. Ueda and Y. Nishiura: “Breathing Scattors in Dissipative Systems”, Progress of Theoretical Physics Supplement No.161(2006)pp364-pp367.
- Y. Nishiura and T. Teramoto : “Collision dynamics in Dissipative Systems”, Theoretical and Applied Mechanics Japan, 59 : 13-25 (2011-03)
- Y. Nishiura and T. Teramoto : “Refraction, Reflection and Splitting”, Far-From-Equilibrium Dynamics, eds. T. Ogawa, K. Ueda, RIMS Kôkyûroku Bessatsu B31: 167-194 (2012-05)
b) Collision of localized traveling convection cells in binary fluids
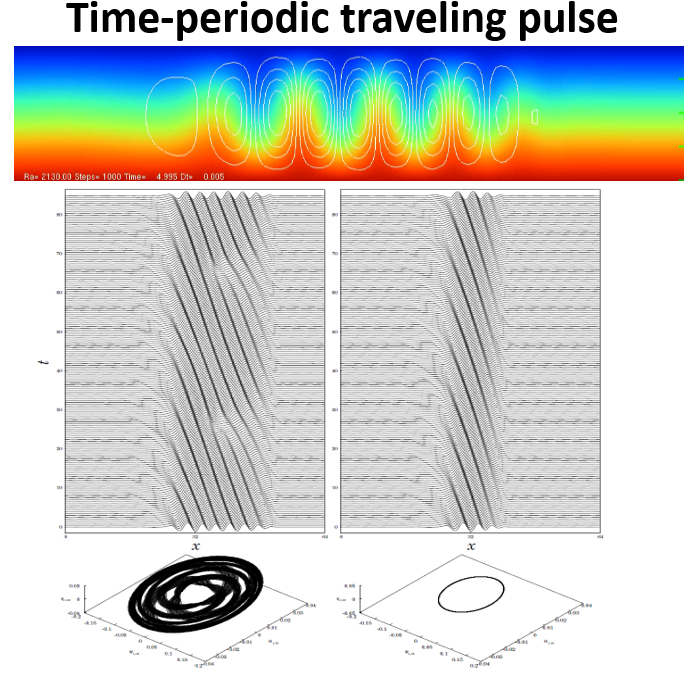
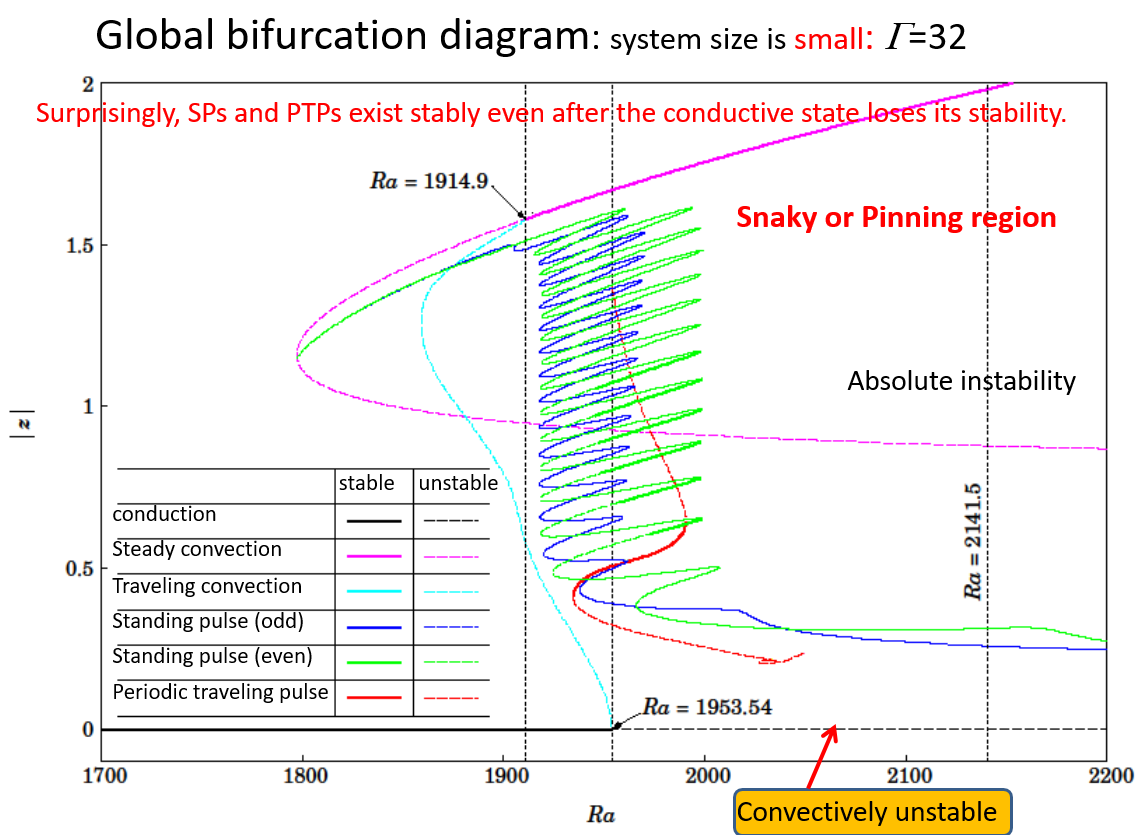
We study spontaneous pattern formation and its asymptotic behaviour in binary fluid flow driven by a temperature gradient [3]. When the conductive state is unstable and the size of the domain is large enough, finitely many spatially localized time-periodic travelling pulses (PTPs), each containing a certain number of convection cells, are generated spontaneously in the conductive state and are finally arranged at non-uniform intervals while moving in the same direction. We found that the role of PTP solutions and their strong interactions (collision) are important in characterizing the asymptotic state. Detailed investigations of pulse–pulse interactions showed the differences in asymptotic behaviour between that in a finite but large domain and in an infinite domain
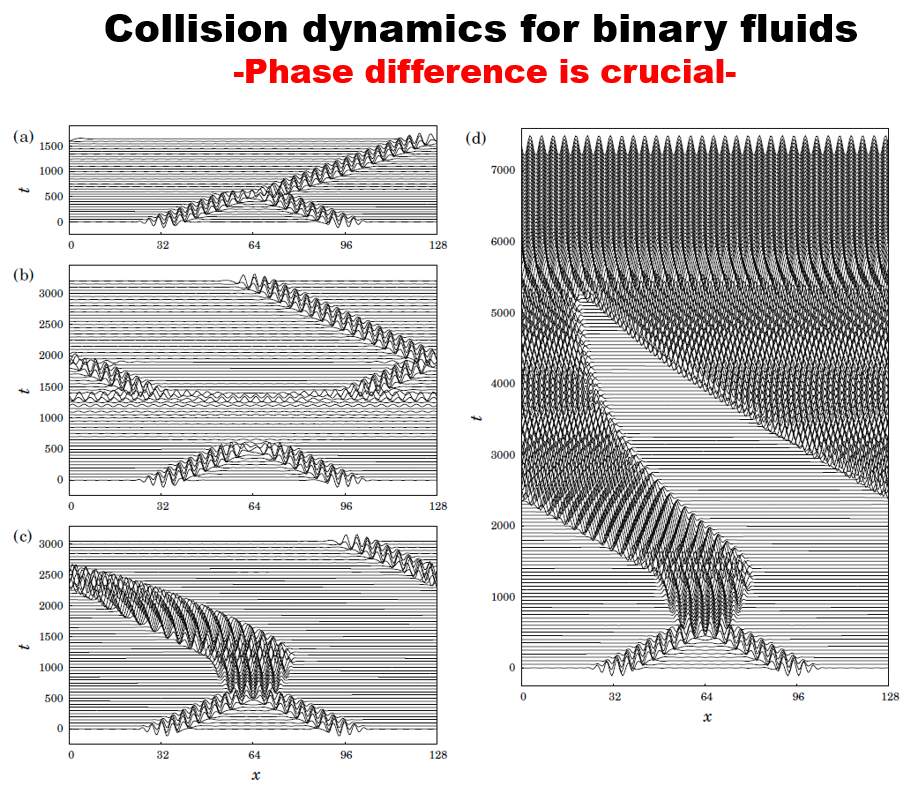
We also study the collision processes of spatially localized convection cells (pulses) in a binary fluid mixture by the extended complex Ginzburg-Landau equations [2]. Both counter- and co-propagating pulse collisions are examined numerically. For counter-propagating pulse collision, we found a special class of unstable time-periodic solutions that play a critical role in determining the output after collision. The solution profile right after collision becomes close to such an unstable pattern and then evolves along one of the unstable manifolds before reaching a final destination. The origin of such a class of unstable solutions, called scattors, can be traced back to two-peak bound states which are stable in an appropriate parameter regime. They are destabilized, as the parameter is varied, and become scattors which play the role of separators of different dynamic regimes. Delayed feedback control is useful to detect them. Also, there is another regime where the origin of the scattors is different from that of the above case. For co-propagating pulse collision, it is revealed that the result of pulse collision depends on the phase difference between pulses. Moreover, we found that the coalescent pulse propagates while maintaining a two-peak bound state, which is not observed in the case of counter-propagating pulse collision. Complicated collision dynamics become transparent to some extent from the viewpoint of those unstable objects.
REFERENCE
- M. Iima and Y. Nishiura: “Collision of localized traveling-wave convection cells in binary fluid“, GAKUTO International Series, Mathematical Sciences and Applications, 22: 289-303 (2005)
- M. Iima and Y. Nishiura: “Unstable periodic solution controlling collision of localized convection cells in binary fluid mixture”, Physica D, 238: 449-460 (2009) DOI: 10.1016/j.physd.2008.11.010
- T. Watanabe, M. Iima and Y. Nishiura: “Spontaneous formation of travelling localized structures and their asymptotic behaviour in binary fluid convection”, Journal of Fluid Mechanics 712: 219-243 (2012)
- T. Watanabe, M. Iima and Yasumasa Nishiura: “A skeleton of collision dynamics — Hierarchical network structure among even-symmetric steady pulses in binary fluid convection —” ,SIAM Journal on Applied Dynamical Systems (SIADS), Vol. 15, No. 2, pp. 789–806 (2016,02,08) DOI:10.1137/15M1010968
3. Propagation in heterogeneous media
Localized waves are one of the main carriers of information and the effect of heterogeneity of the media in which it propagates is of great importance for the understanding of signaling processes in biological and chemical problems. A typical and simple heterogeneity is a spatially localized bump or dent in 1D or 2D, which in general creates associated defects in the media. One of the main issues is how the geometry of heterogeneity influences over the dynamics of waves. Here the geometry means slope, height, size, curvature and so on. Localized waves are sensitive to those factors and in fact present a variety of dynamics including rebound, pinning, splitting, and traveling motion around the defect. A reduction method to finite-dimensional system is presented, which clarifies the mathematical structure for those dynamics.
In the reference below we mainly focus on a class of one-dimensional traveling pulses the associated parameters of which are close to drift and/or saddle-node bifurcations. The great advantage to study the dynamics in such a class is two-fold: firstly it gives us a perfect microcosm for the variety of outputs in general setting when pulses encounter heterogenieties. Secondly it allows us to reduce the original PDE dynamics to tractable finite dimensional system. Such pulses are sensitive when they run into the heterogeneities and show rich responses such as annihilation, pinning, splitting, rebound as well as penetration. The reduced ODEs explain all these dynamics and the underlying bifurcational structure controlling the transitions among different dynamic regimes. It turns out that there are hidden ordered patterns associated with the critical points of ODEs which play a pivotal role to understand the responses of the pulse. We mainly focus on a bump and periodic types of heterogeneity, however our approach is also applicable to general case. It should be noted that there appears spatio-temporal chaos for periodic type of heterogeneity when its period becomes comparable with the size of the pulse [1].
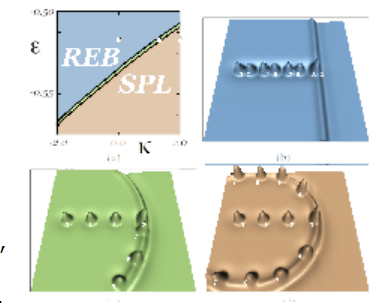
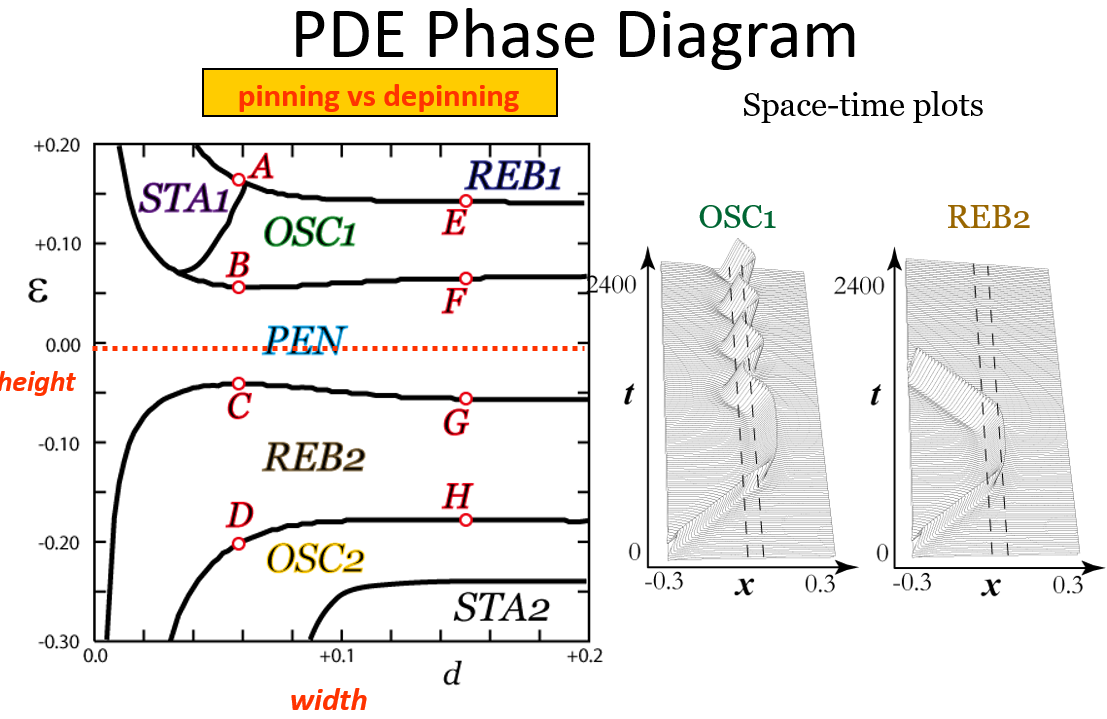
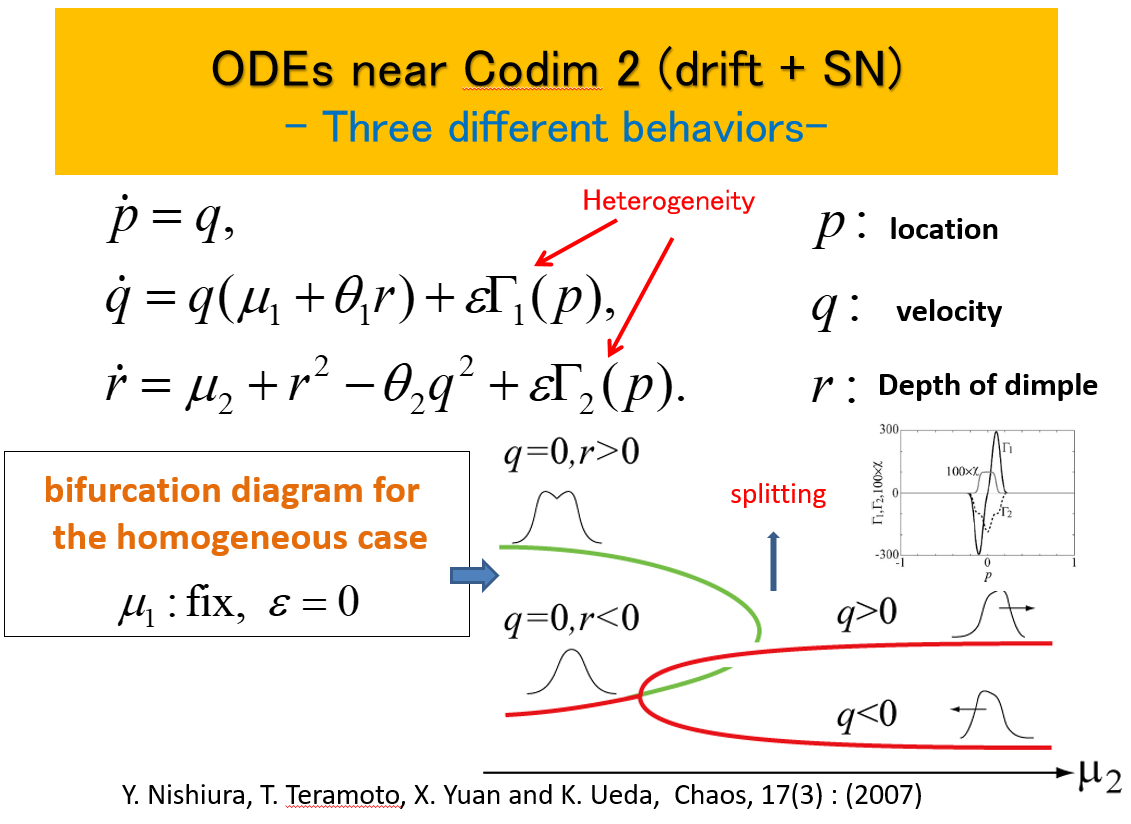
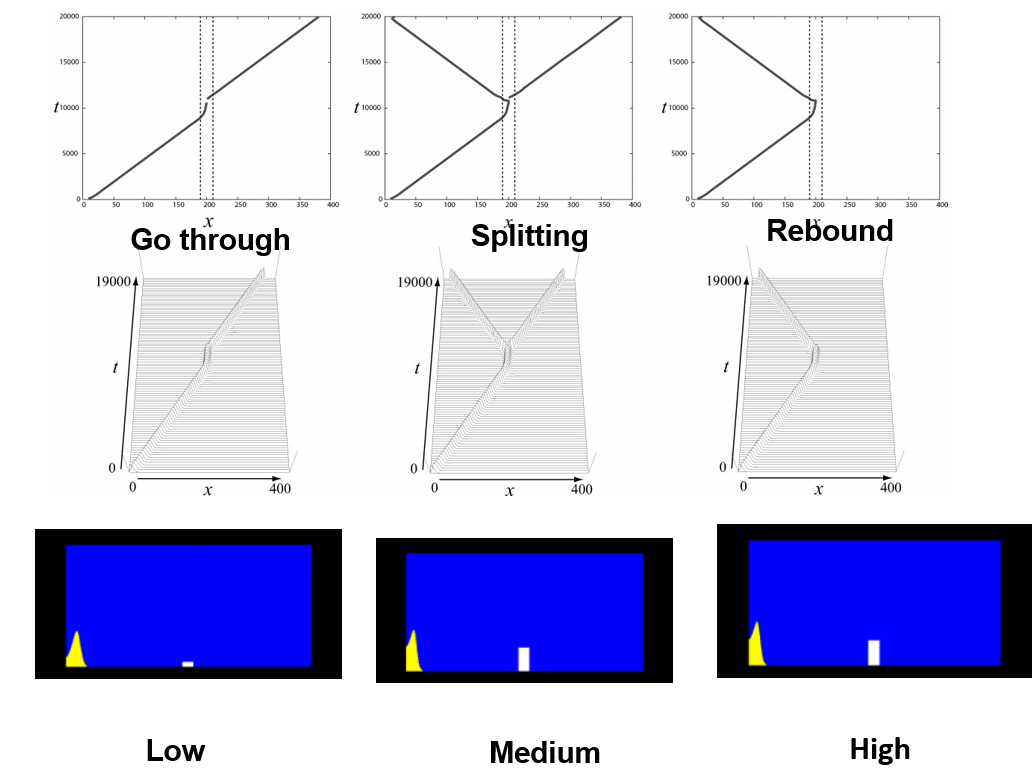
REFERENCE
- Y. Nishiura, T. Teramoto, X. Yuan and K.-I. Ueda: “Dynamics of traveling pulses in heterogeneous media“, Chaos, 17(3) : 037104 (2007)
- X. Yuan, T. Teramoto, and Y. Nishiura: “Heterogeneity-induced defect bifurcation and pulse dynamics for a three-component reaction-diffusion system“, Physical Review E, Vol.75(3), 2007: DOI: 10.1103/PhysRevE.75.036220
- Yasumasa Nishiura, Yoshihito Oyama, and K.-I. Ueda: “Dynamics of traveling pulses in heterogeneous media of jump type”, Hokkaido Math.J.Vol.36, No.1(2007) pp207-pp242.
- T. Teramoto, X. Yuan, M. Baer and Y. Nishiura : “Onset of Unidirectional Pulse Propagation in an Excitable Medium with Asymmetric Heterogeneity”, Phys. Rev. E, The American Physical Society, 79 : 046205-1-046205-16 (2009) DOI: 10.1103/PhysRevE.79.046205
- P. V. Heijster, A. Doelman, T. J. Kaper, Y. Nishiura and K. Ueda : “Pinned fronts in heterogeneous media of jump type”, Nonlinearity, 24(1) : 127-157 (2010-11) DOI: 10.1088/0951-7715/24/1/007
- Y. Nishiura and T. Teramoto : “Refraction, Reflection and Splitting”, Far-From-Equilibrium Dynamics, eds. T. Ogawa, K. Ueda, RIMS Kôkyûroku Bessatsu B31: 167-194 (2012-05)
- Y. Nishiura, T. Teramoto and X. Yuan : “Heterogeneity-induced spot dynamics for a three-component reaction-diffusion system ”, Communications on Pure and Applied Analysis, American Insutitute of Mathematical Sciences, 11(1) : 307-338 (2012-01) DOI:10.3934/cpaa.2012.11.307
- K. Nishi, Y. Nishiura and T. Teramoto : “Dynamics of two interfaces in a hybrid system with jump type heterogeneity”, Japan Journal of Industrial and Applied Mathematics, published on-line (2013-02) DOI:10.1007/s13160-013-0100-x
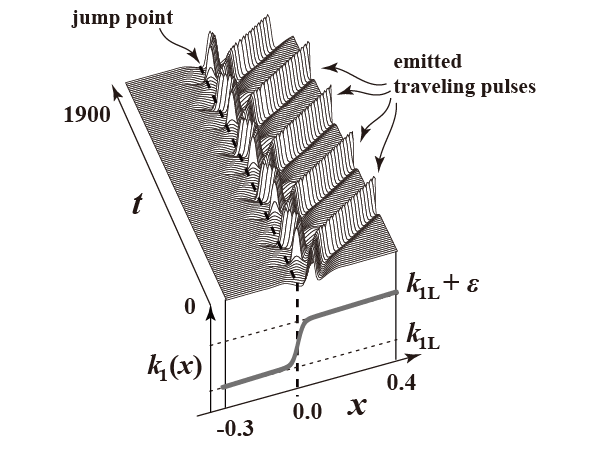
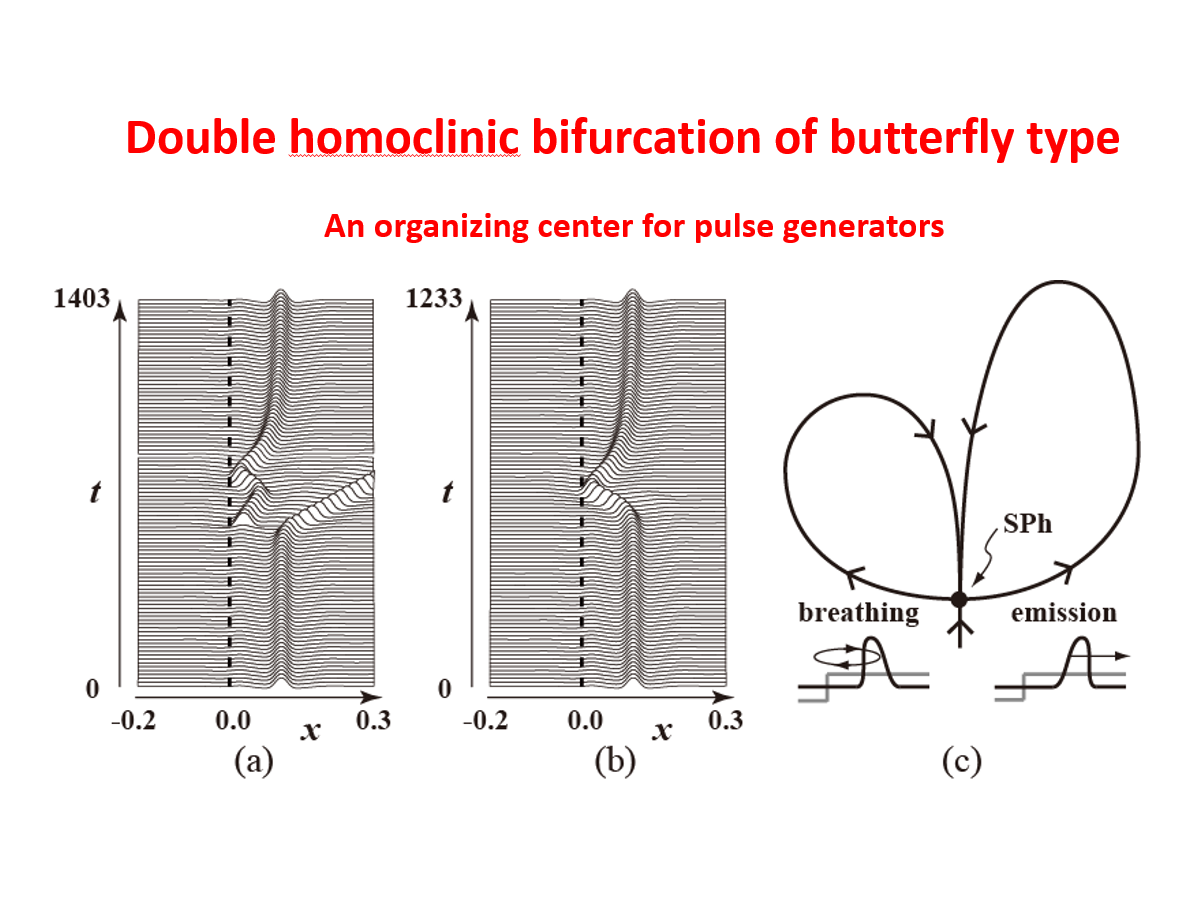
4. Pulse generators
We study a spontaneous pulse-generating mechanism in an excitable medium with jump-type heterogeneity. Such a pulse generator (PG) has attracted considerable interest due to the computational potential of pulse waves in physiological signal processing. We first investigate the conditions for the onset of robust-type PGs, and then we show the global bifurcation structure of heterogeneity-induced patterns, including the complex ordered sequence of pulse-generating manners. We devise numerical frameworks to trace the long-term behavior of PGs as periodic solutions, and we detect the associated terminal homoclinic orbits that are homoclinic to a special type of heterogeneity-induced ordered pattern with a hyperbolic saddle. These numerical approaches assist us in identifying a candidate for the organizing center, and producing a variety of PGs as a codimension-two gluing bifurcation, in which two homoclinic trajectories associated with pulse emission and breathing motions form a butterfly configuration.
REFERENCE
- M.Yadome, Y. Nishiura, T. Teramoto : “Robust pulse generators in an excitable medium with jump-type heterogeneity”, SIAM Journal on Applied Dynamical Systems, Vol.13(3):1168-1201(2014) DOI:10.1137/13091261X
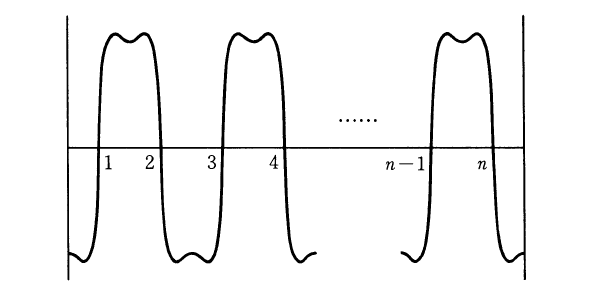
5. Stability of singularly perturbed solutions -the SLEP method –
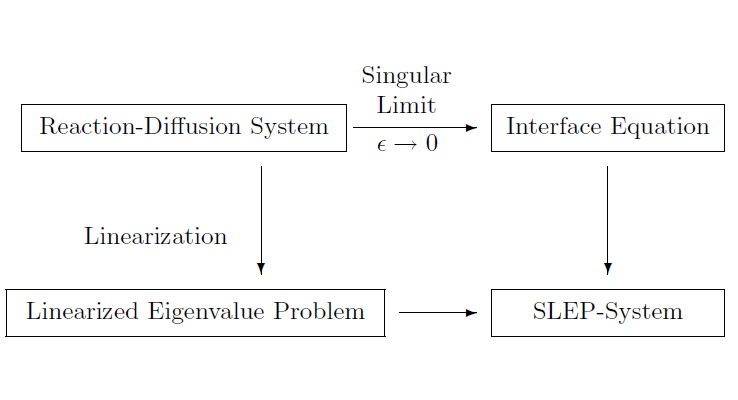
This is about a general analytical method to study the stability properties of large amplitude singularly perturbed solutions arising in reaction diffusion systems on a bounded domain. Such solutions in general have sharp transition layers inside the domain as in the figure below and their linearized problems have finitely many critical eigenvalues proportional to the number of those layers, which converge to zero as the thickness of layer tends to zero. The main difficulty is to show how those critical ones behave near the origin or imaginary axis as thickness goes to zero. The SLEP (singularly perturbed eigenvalue problem) method first developed in [11] is one of the powerful analytical tools to clarify the precise behavior of critical eigenvalues as thickness goes to zero. The associated critical eigenfunctions are characterized as a combination of Dirac’s delta located at layer positions in the singular limit for 1D case. It turns out that the asymptotic behaviors of critical eigenvalues can be obtained by solving a special type of tri-diagonal matrix derived from the Green function of the associated linearized operator (see Lemma 5.38 of the reference [2] and [4] for details). The SLEP method has been applied to a variety of singularly perturbed reaction diffusion systems as shown in the literature below.
The commutative diagram below holds between taking the singular limit and linearization. The extension to the higher dimensional space is also possible as discussed in [1].
REFERENCE
- Y. Nishiura and H. Fujii : “Stability of Singularly Perturbed Solutions to Systems of Reaction-Diffusion Equations”, SIAM J. Math. Anal. 18, : 1726-1770(1987)
- Yasumasa Nishiura and Masayasu Mimura : “Layer Oscillations in Reaction- Diffusion Systems”, SIAM J. APPL. MATH, 49(2) : 481-514(1989)
- H. Ikeda, M. Mimura and Y. Nishiura : “Global Bifurcation Phenomena of Travelling Wave Solutions for some bistable Reaction-Diffusion Systems”, Nonlinear Analysis, Theory, Methods & Applications, 13(5) : 507-526(1989)
- Yasumasa Nishiura and Tohru Tsujikawa : “Instability of singularly perturbed Neumann layer solutions in reaction-diffusion systems”, Hiroshima Mathematical Journal, 20(2) : 297-329(1990)
- Hiroshi Kokubu, Yasumasa Nishiura and Hiroe Oka : “Heteroclinic and Homoclinic Bifurcations in Bistable Reaction Diffusion Systems”, JOURNAL OF DIFFERENTIAL EQUATIONS, 86(2) : 260-341(1990)
- G. Caginalp and Y. Nishiura : “The Existence of Traveling Waves for Phase Field Equations and Convergence to Sharp Interface Models in the Singular Limit”, QUARTERLY OF APPLIED MATHEMATICS, 49(1) : 147-162(1991)
- Masaharu Taniguchi and Yasumasa Nishiura: “Instability of planar interfaces in reaction-diffusion systems”, SIAM J. MATH. ANAL. 25(1) : 99-134(1994)
- Yasumasa Nishiura : “Coexistence of Infinitely Many Stable Solutions to Reaction Diffusion Systems in the Singular Limit”, Dynamics Reported 3 : 25-103(1994)
- Yasumasa Nishiura and Hiromasa Suzuki : “Nonexistence of higher dimensional stable Turing patterns in the singular limit”, SIAM J. MATH. ANAL. 29(5) : 1087-1105(1998)
- Yasumasa Nishiura, “Far-from-Equilibrium Dynamics“,Translations of Mathematical Monographs Iwanami Series in Modern Mathematics, AMS 2002; 311 pp;Volume: 209, ISBN-10: 0-8218-2625-5
- Y. Nishiura and H. Suzuki : “Higher dimensional SLEP equation and applications to morphological stability”, SIAM J. Math. Anal., 36(3) : 916-966 (2005) DOI: 10.1137/S0036141002420157
6. Response of BZ waves to local pulse irradiation
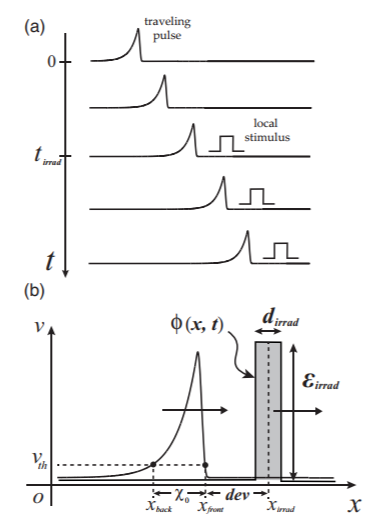
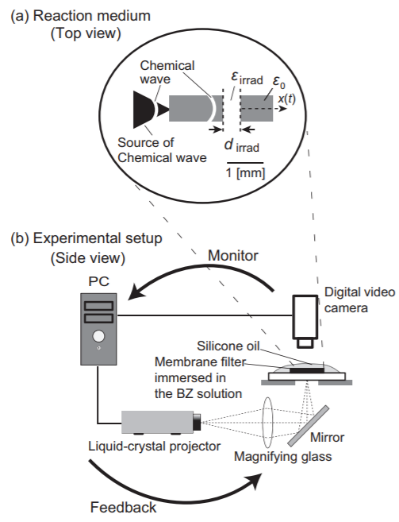
The photo-sensitive Belousov–Zhabotinsky (BZ) reaction system was investigated to understand the response of wave propagation to local pulse stimulation in an excitable field. When the chemical wave was irradiated with a bright pulse or a dark pulse, the speed of wave propagation decreased or increased.
The timing of pulse irradiation that significantly affected the speed of chemical wave propagation was different with the bright and dark pulses. That is, there is a sensitive point in the chemical wave. The experimental results were qualitatively reproduced by a numerical calculation based on a three-variable Oregonator model that was modified for the photosensitive BZ reaction. These results suggest that the chemical wave is sensitive to the timing of pulse irradiation due to the rates of production of an activator and an inhibitor in the photochemical reaction [1].
The response of a traveling pulse to a local external stimulus is considered numerically for a modified three-component Oregonator, which is a model system for the photosensitive Belousov-Zhabotinsky (BZ) reaction. The traveling pulse is traced and constantly stimulated, with the distance between the pulse and the stimulus being kept constant. We are interested in the minimal strength of the spatially localized stimulus in order to eliminate the pulse. The use of a stimulus of small width allows us to detect the point in the pulse most sensitive to the external stimulus, referred to as the “Achilles’ heel” of the traveling pulse, at which minimal strength of stimulus causes a collapse of the pulse. Our findings are demonstrated experimentally as well with the photosensitive BZ reaction [2].
REFERENCE
- Satoshi Nakata, Shogo Suzuki, Takato Ezaki, Hiroyuki Kitahata, Kei Nishi and Yasumasa Nishiura : “Response of a chemical wave to local pulse irradiation in the ruthenium-catalyzed Belousov–Zhabotinsky reaction”, Physical Chemistry Chemical Physics, 17, 9148-9152(2015) DOI:10.1039/C5CP00897B
- Kei Nishi, Shogo Suzuki, Katsuhiko Kayahara, Masakazu Kuze, Hiroyuki Kitahata, Satoshi Nakata,and Yasumasa Nishiura:”Achilles’ heel of a traveling pulse subject to a local external stimulus“, Physical Review E 95, June 2017, DOI: 10.1103/PhysRevE.95.062209,
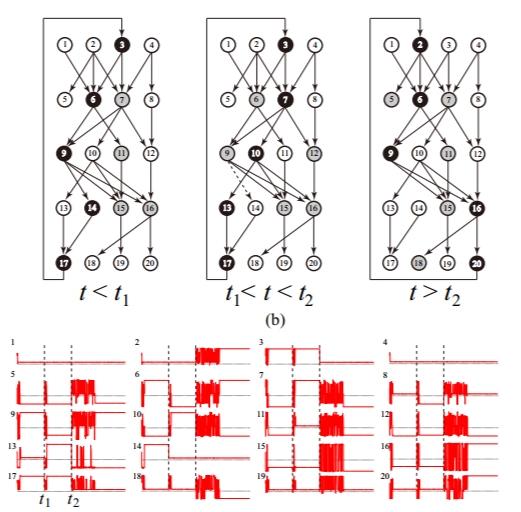
7. Multistate network model for pathfinding problems
We propose a network of excitable systems that spontaneously initiates and completes loop searching against the removal and attachment of connection links. Network nodes are excitable systems of the FitzHugh-Nagumo type that have three equilibrium states depending on input from other nodes. The attractors of this network are stationary solutions that form loops, except in the case of an acyclic network. Thus, the system is regarded as a loop searching system. To design a system capable of self-recovery (the ability to find a loop when one of the connections in an existing loop is suddenly removed), we have investigated regulatory rules for the interaction between nodes and have used two characteristic properties of nonlinear dynamical systems to provide a solution: post-inhibitory rebound phenomena and saddle-node bifurcation.
REFERENCE
- Kei-Ichi Ueda, Masaaki Yadome and Yasumasa Nishiura : “Multistate network for loop searching system with self-recovery property” , Physical Review E, 89(2), 022810 (2014-02) DOI: 10.1103/PhysRevE.89.022810
- Kei-Ichi Ueda, Masaaki Yadome, Yasumasa Nishiura : “Multistate network model for the pathfinding problem with a self-recovery property”, Neural Networks, 62, 32-38 (2015) DOI: 10.1016/j.neunet.2014.08.008
8. Topological approach to materials science
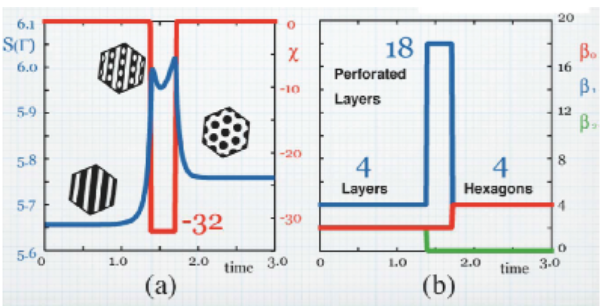
a) Morphological transition of block copolymers and scaling behaviors of Betti number
Block copolymer displays a variety of mesoscopic morphologies including hexagon, gyroid, mesh network, perfolated lamellar depending on composition ratio. Our aim here is to present a new viewpoint for understanding complex dynamics, including morphology transitions, by incorporating topologically invariant quantities, the so-called homological quantities, into the field of materials science, and utilizing them as a means of observation. We measure the topology of a structure by means of its homology, more specifically, we compute its Betti numbers and try to chracterize the transient morphologies when the system is quenched from one state to another.
REFERENCE
- Nishiura, Y., and Ohnishi, I., “Some mathematical aspects of the micro-phase separation in diblock copolymers“, Physica D 84(1995), 31-39.
- Teramoto, T. and Nishiura, Y., ”Double Gyroid Morphology in a Gradient System with Nonlocal Effects”, J. Phys. Soc. Jpn. 71 (2002), 1611-1614.
- Teramoto, T. and Nishiura, Y., ”Double Gyroid Morphology of Diblock Copolymer Problem”, RIMS Kokyuroku No.1356 (2004), 116-121.
- Teramoto, T. and Nishiura, Y.,”Morphology and dynamics of micro-phase separation” (in Japanese), 応用数理15(3): 16-27 (2005)
- T. Teramoto, M. Gameiro and Y. Nishiura : “Applications of computational homology to 3D morphology transitions”, 数理解析研究所講究録, 1614 : 166-171 (2008)
- T. Teramoto and Y. Nishiura : “Morphological characterization of the diblock copolymer problem with topological computation”, Japan Journal of Industrial and Applied Mathematics, 27(2) : 175-190 (2010-09) DOI:10.1007/s13160-010-0014-9
b) Characterization of amorphous state by computational homology
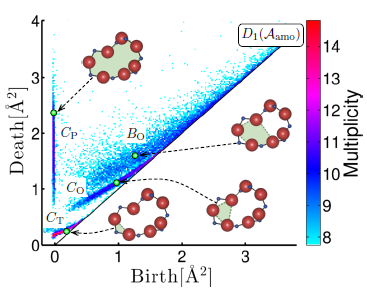
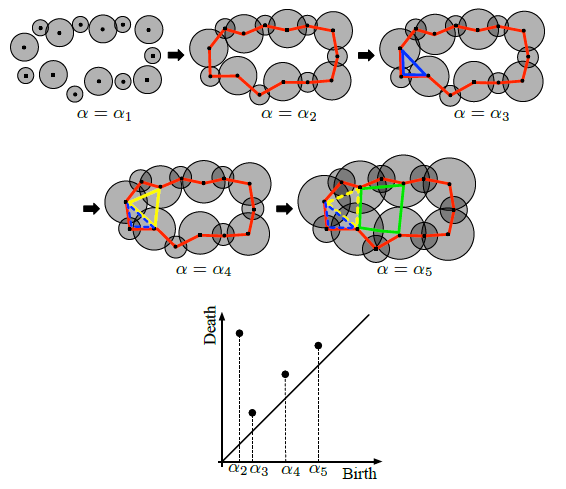
We present a topological method that extracts hierarchical structures of various amorphous solids. The method is based on the persistence diagram (PD), a mathematical tool for capturing shapes of multi-scale data. The input to the PDs is given by an atomic configuration and the output is expressed as two dimensional histograms. Then, specific distributions such as curves and islands in the PDs identify meaningful shape characteristics of the atomic configuration. Although the method can be applied to a wide variety of disordered systems, it is applied here to silica glass, the Lennard-Jones system, and Cu-Zr metallic glass as standard examples of continuous random network and random packing structures.
In silica glass, the method classified the atomic rings as short-range and medium-range orders, and unveiled hierarchical ring structures
among them. These detailed geometric characterizations clarified a real space origin of the first sharp diffraction peak, and also indicated that PDs contain information on elastic response. Even in the Lennard-Jones system and Cu-Zr metallic glass, the hierarchical structures in the atomic configurations were derived in a similar way using PDs, although the glass structures and properties substantially different from silica glass. These results suggest that the PDs provide a unified method that extracts greater depth of geometric information in amorphous solids than conventional methods.
REFERENCE
- Yasuaki Hiraoka, Takenobu Nakamura, Akihiko Hirata, Emerson G. Escolar, Kaname Matsue, and Yasumasa Nishiura: “Hierarchical structures of amorphous solids characterized by persistent homology”, Proceedings of the National Academy of Sciences of the United States of America 113(23) Jun 2016
- Takenobu Nakamura, Yasuaki Hiraoka, Akihiko Hirata, Emerson G Escolar, Yasumasa Nishiura, “Persistent homology and many-body atomic structure for medium-range order in the glass”, IOP Publishing 26(30) 1-13, Jul 2015
- Yasuaki Hiraoka and Yasumasa Nishiura, “Order in Disorder: Persistent Homology and Its Applications”, BUTSURI 72(9) 632-640 (2017) ( in Japanese).
9. Decision making via interaction with environments
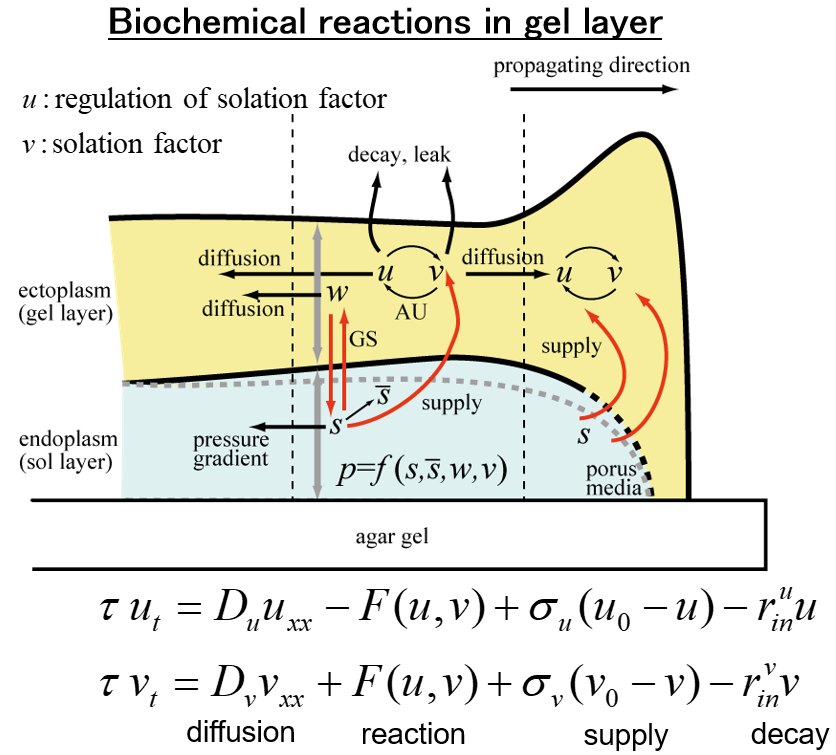
-Behaviors of amoeba (Physarum plasmodium) in heterogeneous environments-
We report here a new kind of behavior that seems to be ’indecisive’ in an amoeboid organism, the Physarum plasmodium of true slime mold. The plasmodium migrating in a narrow lane stops moving for a period of time (several hours but the duration differs for each plasmodium) when it encounters the presence of a chemical repellent, quinine. After stopping period, the organism suddenly begins to move again in one of three different ways as the concentration of repellent increases: going through the repulsive place (penetration), splitting into two fronts of going through it and turning (splitting) and turning back (rebound). In relation to the physiological mechanism for tip migration in the plasmodium, we found that the frontal tip is capable of moving further although the tip is divided from a main body of organism. This means that a motive force of front locomotion is produced by a local process at the tip. Based on this finding, a mathematical model for front locomotion is considered in order to understand the dynamics for both the long period of stopping and three kinds of behavior. A model based on reaction-diffusion equations succeeds to reproduce the experimental observation. The origin of long-time stopping and three different outputs may be reduced to the hidden instabilities of internal dynamics of the pulse, which may be a skeleton structure extracted from much more complex dynamics imbedded in the Physarum plasmodium.

REFERENCE
- T. Nakagaki, R. Kobayashi, T. Ueda and Y. Nishiura: “Obtainning multiple separate food sources: Behavioural intelligence in the Physarum plasmodium“, Proc. R. Soc. Lond. B, 271: 2305-2310 (2004)
- T. Nakagaki, M. Iima, T. Ueda, Y. Nishiura, T. Saigusa, A. Tero, R. Kobayashi, and K. Showalter: “Minimum-Risk Path Finding by an Adaptive Amoebal Network“, PRL99, 068104 (2007)
- Takagi Seiji, Nishiura Yasumasa, Nakagaki Toshiyuki, Ueda Tetsuo and Ueda Kei-ichi: “Indecisive behavior of amoeba crossing an environmental barrier“, Proceedings of Int. Symp. on Topological Aspects of Critical Systems and Networks, World Scientific Publishing Co. 86-93 (2007)
- Takagi Seiji, Nishiura Yasumasa, Nakagaki Toshiyuki, Ueda Tetsuo and Ueda Kei-ichi: “Indecisive behavior of amoeba crossing an environmental barrier”, Proceedings of Int. Symp. on Topological Aspects of Critical Systems and Networks, World Scientific Publishing Co. 86-93 (2007). (This is about the response of amoeba when it propagates and encounters with toxic (heterogeneous) area.)
- K.-I. Ueda, S. Takagi, Y. Nishiura and T. Nakagaki : “Mathematical model for contemplative amoeboid locomotion”,Physical Review E, 83(2) (2011-02) DOI: 10.1103/PhysRevE.83.021916
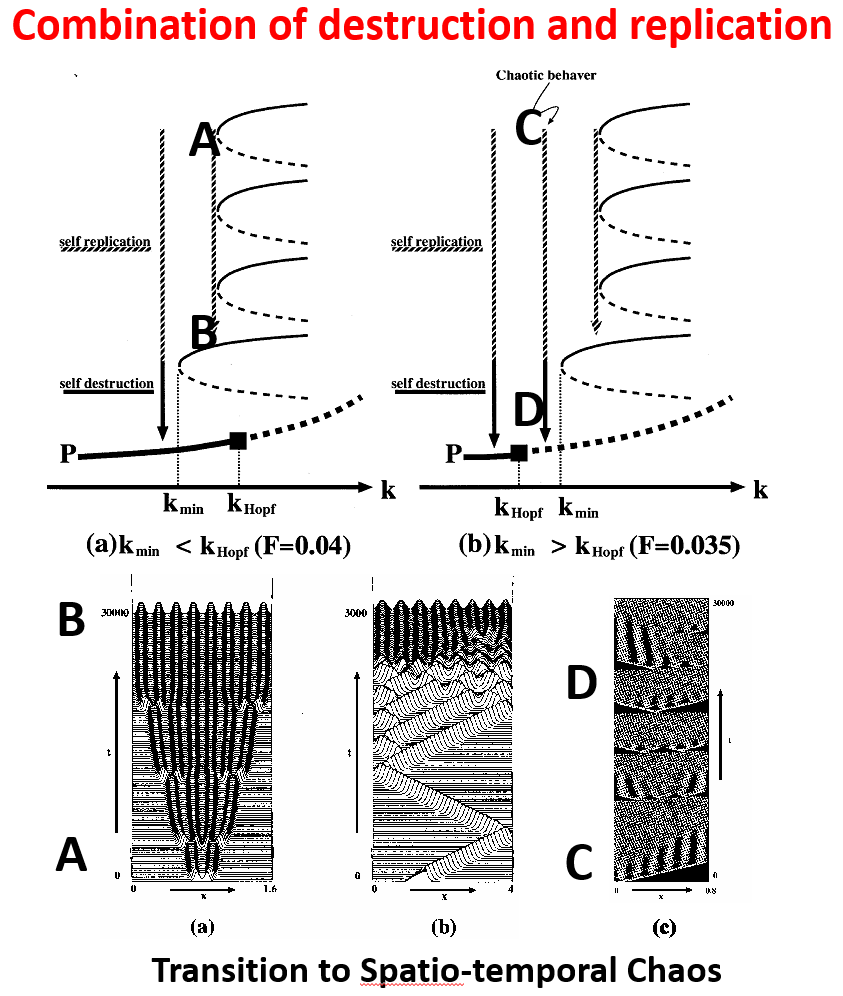
10. Self-replication, spatio-temporal chaos, and propagation failure
Self-replicating patterns (SRP) have been observed in several chemical reaction models, such as the Gray–Scott (GS) model, as well as in physical experiments. Watching these experiments (computational and physical) is like watching the more familiar coarsening processes but in reverse: the number of unit localized patterns increases until they fill the domain completely. Self-replicating dynamics, then, can be regarded as a transient process from a localized trigger to a stable stationery or oscillating Turing pattern. Since it is a transient process, it is very difficult to give a suitable definition to characterize SRP. It cannot be described in terms of well-studied structures such as the attractor or a singular saddle orbit for a dynamical system.
In this paper, we present a new point of view to describe the transient dynamics of SRP over a finite interval of time. We focus our attention on the basic mechanism causing SRP from a global bifurcational point of view and take our clues from two model systems including the GS model. A careful analysis of the anatomy of the global bifurcation diagram suggests that the dynamics of SRP is related to a hierarchical structure of limit points of folding bifurcation branches in parameter regions where the branches have ceased to exist. Thus, the skeleton structure mentioned in the title refers to the remains of bifurcation branches, the aftereffects of which are manifest in the dynamics of SRP. One of the natural and important problems is about the existence of an organizing center from which the whole hierarchical structure of limit points emerges. In our setting, the numerics suggests a strong candidate for that, i.e., Bogdanov–Takens–Turing (BTT) singularity together with the presence of a stable critical point, and so this indicates a universality of the above structure in the class of equations sharing this characteristic.
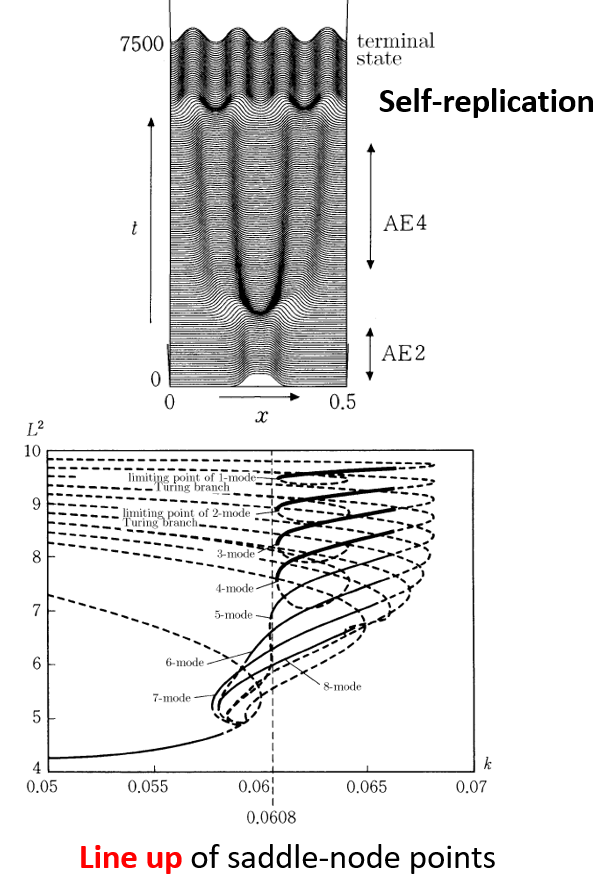
A new geometrical criterion for the transition to spatio-temporal chaos (STC) arising in the Gray–Scott model is presented. This is based on the inter-relationship of global bifurcating branches of ordered patterns with respect to supply and removal rates contained in the model. This viewpoint not only gives us a new criterion for the onset of STC but also clarifies how the orbit itinerates among several ordered patterns in infinite-dimensional space. Moreover, the geometrical characterization gives us a universal viewpoint about the onset and termination of STC. There are at least two different mechanisms that cause re-injection dynamics and drive the STC: one is a generalized heteroclinic cycle consisting of self-replication and self-destruction processes, and the other involves annihilation of colliding waves instead of self-destruction.
REFERENCE
- Y.Nishiura and D.Ueyama, “A skeleton structure of self-replicating dynamics“, Physica D 130(1999),73-104.
- S. Ei, Y. Nishiura and K. Ueda: “2n-splitting or Edge-splitting -A manner of splitting in dissipative systems“, JJIAM, 18(2): 181-205 (2001)
- Y. Nishiura and D. Ueyama: “Spatio-temporal chaos for the Gray-Scott model“, Physica D, 150: 137-162 (2001)
- Y. Nishiura, D. Ueyama and T. Yanagita: “Chaotic pulses for discrete reaction diffusion systems“, SIAM Journal on Applied Dynamical Systems 4(3): 733-754 (2005)
- T. Yanagita, Y. Nishiura and R. Kobayashi: “Signal propagation and failure in one-dimensional FitzHugh-Nagumo equations with periodic stimuli“, Phys. Rev. E, 71(3): 6226-6230 (2005)
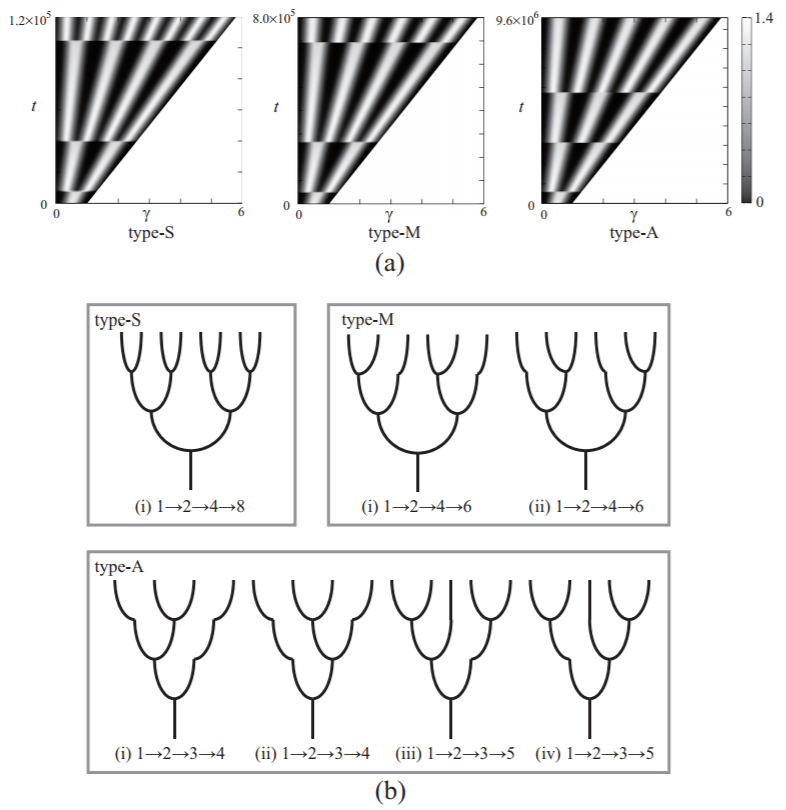
11. Patterns on a growing domain
A cascade process involving stripe splitting in reaction-diffusion systems with isotropically growing one-dimensional domains is studied. Such cascades, propagating from a smaller domain to a larger domain, have been proposed as an answer to the criticism that the Turing mechanism lacks robustness because many stable patterns can coexist on a large domain and, therefore, the final state is very sensitive to the initial conditions. In contrast, if the system starts with a small domain, very few stable patterns are possible, which limits the sensitivity to the initial conditions. In order to show the validity and limitations of this scenario, we clarify the underlying mathematical mechanism that drives various types of stripe-splitting via a reduction from partial differential equations to ordinary differential equations, as well as investigating global arrangements of the set of n-mode stripe branches with Dn-symmetry of the stripe locations. The mathematical simplification above allows us to reveal how each n-mode stripe branch is destabilized as the domain grows and to characterize the associated eigenprofiles that actually determine the manner of splitting at the infinitesimal level. We find that all the Dn-symmetry-breaking instabilities typically occur simultaneously up to leading order before the saddle-node point of the n-mode stripe branch is reached. The instability with the largest real part is of the alternate type: every other peak splits at the infinitesimal level. A symmetry-preserving instability appears at the saddle-node point, which drives the simultaneous type of splitting, i.e., mode-doubling. Due to competition between these two types of instabilities, the problem depends subtly on the growth speed. Alternate splitting typically arises for slow growth and simultaneous splitting for fast growth. For intermediate growth rates, the manner of splitting becomes mixed and sensitive to fluctuations.
REFERENCE
- K.-I. Ueda and Y. Nishiura : “A mathematical mechanism for instabilities in stripe formation on growing domains”, Physica D: Nonlinear Phenomena, Elsevier, 241 : 37-59 (2012-01) DOI:10.1016/j.physd.2011.09.016
12. Inhibitory or repulsively coupled oscillators
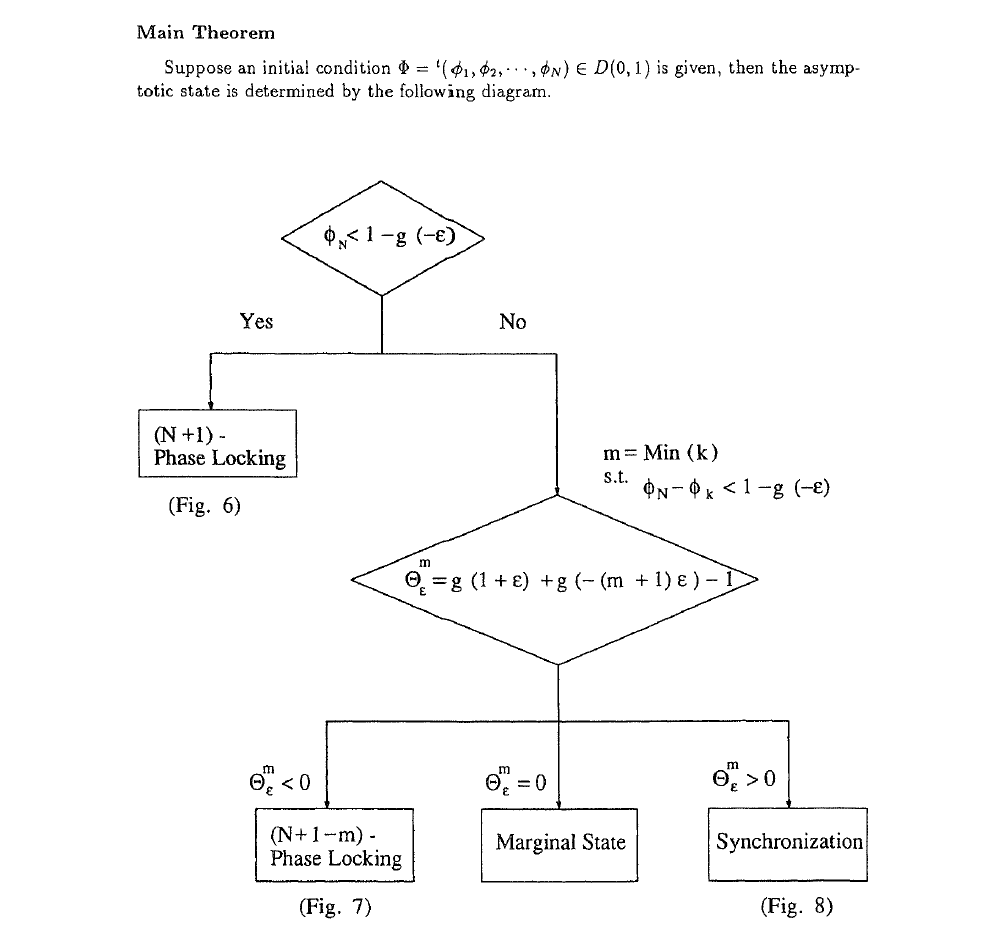
a) Dynamics of inhibitory pulse-coupled oscillators [1]

See the following paper for a good review in this direction.
Eugene M. Izhikevich: “Weakly Pulse-Coupled Oscillators, FM Interactions,
Synchronization, and Oscillatory Associative Memory”, IEEE TRANSACTIONS ON NEURAL NETWORKS, VOL. 10, NO. 3, MAY 1999
b) Switching behaviors for repulsively coupled oscillators [2]
We study intermittent switching behaviors in a system with three identical oscillators coupled diffusively and repulsively, to clarify a bifurcation scenario which generates such intermittent switching behaviors. We use the Stuart-Landau oscillator, which is a general form of Hopf bifurcation, and can describe both cases: limit cycle and inactive i.e., non-self-oscillatory cases. From a numerical study of the bifurcation structure, two different routes to chaos which has S3 symmetry were found. One is the sudden appearance of chaos as PomeauManneville intermittency, which is found for the inactive case. In this case a trajectory shows switching among three mutually symmetric tori when a parameter exceeds critical value. The other route, which appears for the limit cycle case, consists of two parts: First, chaos with lower symmetry appears through period doubling, and after the two successive attractor-merging crises, chaos which has S3 symmetry appears. At each crisis, the attractor changes its symmetry.
REFERENCE
- Y. Nishiura, J. Shidawara, T. Takaishi, “Dynamics of inhibitory pulse-coupled oscillators, in Dynamical Systems and Applications“. Singapore, World Scientific, 1995.
- K. Ito and Y. Nishiura, “Intermittent switching for three repulsively coupled oscillators“, PRE, Phys. Rev. E 77, 036224 (2008)

Editors
I am currently serving as an associate editor of the following journals:
- Physica D
- SIADS (SIAM Journal on Applied Dynamical Systems)
- Multiscale Modeling and Simulation: A SIAM Interdisciplinary Journal
- (Series editor) Mathematics of Planet Earth, Springer: http://www.springer.com/series/13771
Also I worked as the program director of JST Math Program from 2007 to 2016: http://www.jst.go.jp/crest/math/