

AIMR recognizes the importance of the following subjects in the field of materials science in future generations, and has turned the spotlight on these themes by positioning them as the Center’s Three Target Projects. By conducting careful and detailed investigation into these fields with the help of higher mathematics, researchers aim to elucidate common principles and uncover the mechanisms behind each phenomenon.

This project studies the structure and physical properties of materials such as metallic glass and polymers, investigates their stability, and elucidates the mechanisms behind the formation of such material structures. The aim of the project is to discover new functions based on common principles of non-equilibrium states.
Materials and devices that can contribute to the creation of a "green" society, such as metallic glass, polymer glass, block copolymers, biomimetic materials, and super-hybrid functional devices.
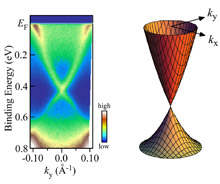
This project places the focus on topics such as functions that have their origins in electron "spin" and "topology of energy band," and the relationship between "topology" and the activity demonstrated by nanoporous metal catalyst. The aim of the project is to create topological materials with robust properties, and which are able to adapt to changes in the environment.
Spintronics materials, superconductors, MEMS devices, and nanoporous metal catalysts that can contribute to energy saving, as well as new materials for photovoltaic energy conversion (solar cells) and thermoelectric conversion, which can be applied to energy harvesting.

Materials with innovative functions are created based on an understanding of hierarchical structures of materials ranging from the atomic and molecular level to macroscopic bulk materials. In other words, an understanding of hierarchical structures is necessary at all levels, including the short-range order (nanoclusters), long-range order (nanocrystals), crystalline, and polycrystalline levels. It is important to bridge the various scales and acknowledge the importance of functions identified in multi-scale structures, and the key lies in the size interface (connections between different scales) and spatial interface (grain boundaries, etc.).
The goal of the project is to understand the mechanisms behind functional discoveries through investigations into the interface processes ranging from the atomic and molecular level to properties at the macro level. By creating hierarchical structures, the project also aims to elucidate the relationship between the mid-range and long-range order observed in atomic and molecular cluster domain arrays, with their functional discovery, through their relationship with hierarchies. Examples of research subjects under the umbrella of this project include research on grain boundaries aimed at improving electrical conductivity in devices, research on solid-liquid interfaces aimed at resolving friction issues, which are of great importance in energy saving, research on nanoporous and super-capacitors for energy storage, and research on biomimetic materials.
In order to achieve the goals set out in three target projects, we have made efforts to strengthen the collaboration between mathematics and materials science. Two professors have been appointed as Principal Investigators (PI) in the Mathematics Unit, and project leaders and sub-leaders have been assigned to each project. The leaders and sub-leaders have organized several study groups in relation to each of these projects. In FY2011, an open recruitment of interfacial researchers was conducted worldwide, and six researchers were selected from among 68 applicants. These six researchers are theorists, and are not attached to any particular PI. Rather, they are engaged in research activities together with several experimental laboratories, and utilize their mathematical and theoretical knowhow to introduce new ideas to the research subjects. They also contribute to discussions pertaining to the outcome of experiments, and provide suggestions for new approaches to material control. These interfacial researchers play a significant role in facilitating communication between mathematicians and experimental materials researchers.