

Kelvin’s Conjecture and Experiments of Soap Films
Dr. Chie Nara
(Meiji Institute for Advanced Study of Mathematical Sciences, Meiji University)
December 16 (Fri), 2016 14:30-15:30
Seminar Room, 2nd floor, WPI-AIMR Main Bldg.
How can space be divided into cells of equal volume so as to minimize the (average) surface area of the boundary? In 1887, Lord Kelvin (William Thomson) conjectured that the partition made by a packing of congruent copies of the truncated octahedron with slightly curved faces is the solution (see Figure 1). His conjecture is based on the rules of Plateau (1873) in the theory of foams (see Figure 2). In1994, Denis Weaire, an Irish physicist, and Robert Phelan showed a counterexample to Kelvin’s conjecture, in which packing consists of two kinds of cells with curved faces.
If we restrict cells to space-fillers, congruent polyhedral tiles, we get the orthic version of Kelvin’s conjecture; the truncated octahedron has the minimum surface area among all polyhedral space-fillers. This conjecture is still open. In this paper we introduce the notion of doubly-covered polyhedra and their unfoldings, which leads to an approach for a partial solution of the new Kelvin’s conjecture.
 |
 |
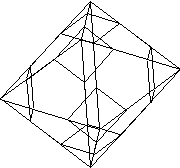
|
| Figure 1. A truncated tetrahedron | Figure 2. Soap films obtained by a rectangular parallelepiped frame |
International Affairs Center (IAC), AIMR
| Address : | 2-1-1, Katahira, Aoba-ku, Sendai, 980-8577 |
|---|---|
| TEL : | +81-22-217-5971 |
| E-MAIL : | iac@grp.tohoku.ac.jp |