本CREST研究の概要
研究の目標
本CREST研究は、臨床医療の現場に数理モデリングの考え方と方法論を広く導入し、臨床医療への数学からの貢献と、数学自身の発展の両方を目指して進めています。主な目標は、下記の4点です。
- 本CREST研究では、医療現場において機序(メカニズム)が明確になっていない様々な現象に適切な数理モデルを導入することによって、臨床医の助けとなるツールを提供することを第一のねらいとしています。ここでいう「ツール」とは蓄積された診断アルゴリズムとそのためのデータ、コンピュータソフトウェア、及びその背後にある数学的技術の全体を指しています。医師が臨床現場で下す診断にあたって判断材料の一つとなるツール群を提供することで、医師個人への負担を軽減し、臨床医療の高度化をもたらすのが本CREST研究の社会貢献上の重要なインパクトになります。また、臨床医療は個々の体を対象としていますがその個人差は大きく、その違いを少ない数のパラメータで表現することは困難です。しかし、形状の差が病態の差につながっていると考えられるケースは多く、その差をどのように表現するのが最も適切か、というのは本質的な問題です。本CREST研究では、先のCREST研究においてその端緒が得られた幾何学的な取り扱いをさらに進め、臓器等の形状表現に対する数理モデルを構築することをねらいとしています。
- 現代の医療現場においては、CTやMRIなどに基づく画像診断が大きな役割を果たしています。解像度や撮影速度の面において機器が急速に進歩し、大量の情報が得られるようになってきていますが、画像に含まれる全ての情報を活かし切れているとは言い難いところがあります。また、内視鏡手術等においては、限られた視野からの画像情報を補完するために、手術前のCTなどの異なる情報の利用を考慮しなければならないなど、技術の進歩に伴う困難も増加しています。本CREST研究では、これらの領域にも画像処理に関する数理モデルを導入することで、より高度な画像診断やリアルタイムの手術支援を実現することもねらいとしています。
- 前項に挙げた画像診断やその他の臨床診断に際しては、経験を積んだ熟練医の判断が重要ですが、そのような画像や臨床データから直接ニューラルネットワーク、サポートベクターマシンなどの機械学習によって何らかの判断を下そうとする試みが近年広く行われており、一定の成果を挙げています。 しかし、こうした手段だけではそこに内包される論理を理解するには不十分であり、新しい知見の追加による医療技術の進化に追随することが困難です。本CREST研究では、様々な手法を用いた学習によって熟練医の経験をアルゴリズム化し、そこに内在する論理構造を明確にすることを目指しています。また、無数の患者を相手にする臨床医療においては、統計的な見方が欠かせません。多くのデータの中から意味のある結果を抽出し、かつその意味の程度までをも正確に記述する統計数学の果たす役割は大きいものです。統計数学は医薬品の評価や疫学などにおいてはすでに重要な役割を果たしていますが、本CREST研究では、臨床医療現場における統計数学の最先端の成果の活用をもねらいとしています。
- 数値シミュレーション結果を用いた可視化画像は一見いかにもそれらしいものであっても、その数学的基礎付けが不完全な部分も数多く残されています。数学的にはどこまでが正しいと保証(または推測)できるのかを検証し、さらに、前提とされている数学的仮定と現実の計算条件との関係を明確にすることで、シミュレーション結果に対する信頼性を確保する必要があります。その成果は、数値シミュレーション技術の向上につながるばかりでなく、臨床医療に限らず広範囲の科学技術上の重要なインパクトとなります。また、臨床医療に現れる諸問題を数学的に定式化し数値シミュレーションを行う場合、単純な理論の適用では、対象が既存の数学の枠組みにおさまらない事態がしばしば起こります。そのような対象に対してひとつずつ理論を整理し、新たに数学的な枠組みを構築していくことは、数学理論の深化を様々な方向に誘発し、現実問題から数学の進歩が促される典型的な例となるものです。本CREST研究ではこの点も重要なねらいとしています。
本CREST研究の柱と他分野との関係
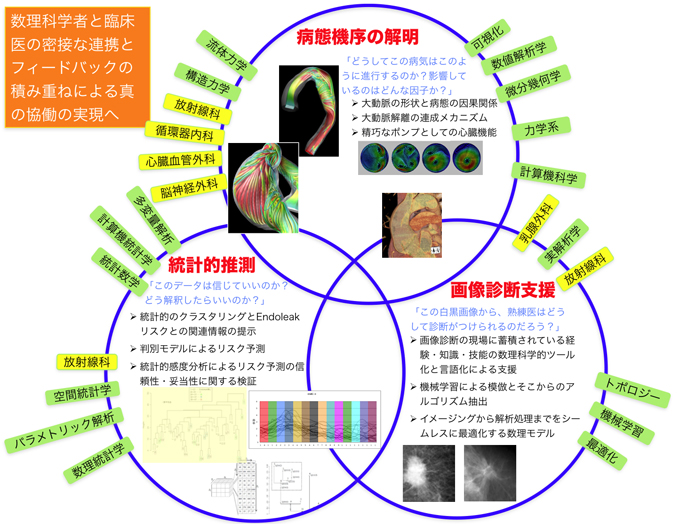
研究項目
テーマA 病態メカニズムの数理モデル化と診断・治療に適した形状表現の数理モデル構築
本研究項目では、様々な病態に対する数理モデル構築とそれに基づく数値シミュレーションを実施し、臨床医との議論を通して、医学的に妥当な数理モデルとして完成させていく。具体的な対象としては、臨床医学から持ち込まれる様々な課題に柔軟に対処するが、まずは、先のCREST研究から引き続いて心臓血管系の疾患、特に大動脈瘤や大動脈解離に関するメカニズム研究を推進する。これらの心臓血管系の病態については、個人差の大きい血管形状を幾何学的な概念を用いて特徴付けし、具体的な病態との関係性を示してきた。本CREST研究ではこれらの取り組みをさらに発展させ、全身血管系ネットワークモデルとの接続、局所的な表面形状に対するガウス曲率、平均曲率等を用いた特徴付けなどを進める。滝沢チームでは、これまでの実績に基づいて先進的な離散化手法や流体構造連成計算の手法構築をさらに進め、水藤チームではそれらを用いたシミュレーションを行い、植田チームから提示されるclinical questionに答えられるような数理モデルとして完成させていく。また、先のCREST研究では流体力学の部分に重点を置いて研究を進めて来たが、現実の心血管系の問題を考える際は、構造力学の問題が非常に重要になることが明らかになってきた。本CREST研究ではその部分についても、生体の特徴を捉えた構造力学をベースとした数理モデルとして構築していく計画である。
テーマB 医用画像のイメージングと解析処理による情報抽出に関する数理モデル構築
本研究項目では、医用画像のイメージングと解析処理による診断と手術の支援に関する研究を扱う。先のCREST研究では、血管造影画像から得られた腸間膜内の動脈のトポロジカルなデータを用いて腸間膜の折り畳まれ方を推定し、内視鏡下手術の安全性向上に役立てる研究を進めて来た。本課題では、これを端緒として医用画像から臨床上有用な情報を最大限に抽出するため、イメージングから解析処理までをシームレスに最適化する数理モデルの構築を行う。具体的には、様々な物理パラメータを取得可能なMRIおよび高精細な形態情報を得ることができるCTを用いて、①画像診断における特徴量となる形態・機能情報、②リアルタイム手術支援など、画像誘導治療に必要な解剖学的構造情報、特にトポロジカルな情報、を抽出するための数理モデル構築を進める。ここで言う数理モデルとは、イメージングにおける信号値モデル、解析処理における情報空間の変換アルゴリズムや、3次元構造から低次元のネットワーク構造を抽出するためのトポロジー処理のアルゴリズムなどを含む。
テーマC 統計的手法を用いた診断アルゴリズムの抽出及び臨床現場に適した統計モデルの構築
本研究項目においては、種々の統計的手法を用いて、臨床医療で使用可能な統計数理モデルを構築する。具体的な対象としてまず取り上げるのは、先のCREST研究においてその端緒が得られている、①スクリーニング検査に対する統計数理モデル、②熟練医の診断アルゴリズム抽出、のふたつである。①については、臨床や疫学の現場でも用いられている統計モデルに対して、最近の統計分野の成果である外れ値の扱い方に関する概念や多くの分野で注目されている変化点検出に関する概念を、新たな視点から導入することで、より現実に即したモデルが得られることが期待できる。②については、classification treeやリサンプリングに関する概念を用いることで、現状では言語化されていない熟練医の頭の中にある論理を適切に抽出し、抽出された論理を後輩医師に伝承することを容易とするものである。
テーマD 臨床現場に適用する種々の数理モデルに対する数学的基盤の確立
本研究項目では、現象論的な立場からの数理モデル(微分方程式系)と数値シミュレーションの仲立ちの役割を果たす、計算モデル(数理モデルをさらに計算を前提に再定式化したもの)の数学的研究を行う。すなわち、現状ではシミュレーションの専門家のノウハウの蓄積によって行われている数値シミュレーションを、個人の経験に依存しない信頼性の高い技術として確立するために、計算モデルを柱と考え数学的な理論の構築を行う。これは、先のCREST研究で、例えば、心血管系の問題を解くにあたって現れた流出境界条件や一般Robin境界条件解析のために、新しい関数空間の研究の必要が生じ、結果的に新しい数学的問題を提示できたことを想定している。より具体的には、水藤チーム・滝沢チームで使われている流体(血液)・構造(血管壁)連成モデルの解析が中心的課題となる。特に、構造物の形状を表現するための仮想領域法や埋込境界法、さらに、最新の数値計算法であるNURBS (Non-Uniform Rational B-Spline)を用いたIGA (Isogeometric Analysis) と呼ばれる離散化手法(この方法では形状の表現と方程式の離散化が一体になっている)は、継続される課題であり、本CRESTでのはじめの対象となる。埋込境界法は、血流シミュレーションでかなりポピュラーな方法であるが、実は、その数学的正当性は(問題のwell-posednessでさえも)わかっていない。これまでの解析で、有界なRadon測度をデータに持つ偏微分方程式として定式されることがわかっている。純粋に数学的な動機で、Radon測度をデータに持つ楕円型方程式の研究は活発である。したがって、具体的な計算への応用の立場から、解析の専門家を巻き込んで、その流体方程式への拡張や離散化の研究を行うことになる。なお、この問題意識は、医療画像を用いた、より幅広い数理的扱いに応用できる可能性があり、本サブテーマにおいてはそのような発展についても検討していく。また、先のCREST研究では、IGAについてその数学的な正当性を保証するために、精度保証付きの数値計算が利用できることを明らかにしてきた。すなわち、証明のためのツールとしての精度保証付き数値計算である。より詳細な解析を進めるためには、精度保証のCREST研究チームと協働して、計算のためのツールを開発する必要がある。また、臨床医療の問題に現れる数値シミュレーションには、未知の生体パラメータを同定するために最適化の考え方がしばしば現れるが、この手法についても新しいアイデアが種々提出されてきており、数学的な課題も多い。これらを磨き上げていくには、幾何、解析などの分野との協働が必須であり、本CREST研究チームには明示的には含まれない多くの数学者(特に純粋数学者)に対しても研究上の働きかけを行っていく所存である。