Speaker Details
In construction...

Senja Barthel
Vrije Universiteit Amsterdam
Webpage
Weaving with periodicity in one dimension: braids
Weavings in one dimension can be described as braids. This talk presents and compares the results of different generative models of classes of braids that might have some relevance for entanglements of 1-dimensional coordination polymers.
Abhijit Champanerkar
The City University of New York
Webpage
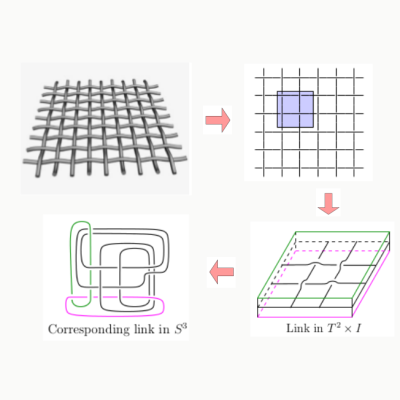
Geometric and diagrammatic maximality of weaving knots
We explore the infinite square weave from two interestingdirections - geometric and diagrammatic. A weaving knot is a closure of a finite piece of the square weave. The hyperbolic geometric of weaving knots gives a geometric measure called the volume density, and the diagrammatic study of weaving knots give a measure of complexity called the determinant density. We study the asymptotics of both these densities and show that they converge to the same number - which is maximal and related to Catalan's constant. This is joint work with Ilya Kofman and Jessica Purcell.

Myfanwy Evans
University of Potsdam
Webpage
Triply-periodic tangling
Using periodic surfaces as a scaffold is a convenient route to making periodic entanglements. I will present a systematic way of building new tangled periodic structures, using low-dimensional topology and combinatorics, posing the question of how to characterise the structures more completely.

Stephen Hyde
The University of Sydney
Webpage
Tangled Polyhedra (co-author: Myf Evans)
Knotted graphs are fascinating objects, with all the complexities of knots and more. We recently found some beautiful embeddings of well known "polyhedral" graphs which are (i) non-trivially knotted and (ii) maximally symmetric. Those graphs correspond to the edge-nets of the Platonic polyhedra - the tetrahedron, octahedron, cube, dodecahedron and icosahedron. (To help with the analysis, we also allow "theta-graphs" with a pair of three-valent vertices joined by three edges and "theta_z-graphs", with a pair of z-valent vertices and z edges, where z=4 and 5.) Our embeddings realise conditions (i-ii) above. They are built as windings of multi-stranded helices on the edges of symmetric embeddings of hyperbolic "polytori", whose genera (g) exceed 1. The relevant polytori are very simple: they can be thought of as tubifications of the edges of the Platonic polyhedra (giving g equal to 2,3,4,5,7,11 and 19). Those embedded polytori have the symmetries of their underlying polyhedral skeletons; winding them with helices leaves branched multi-helical windings with less symmetry. Tuning of the number of strands in the helices and their helical twists induces these special - maximally symmetric - embeddings of graphs whose topologies are exactly those of the Platonic polyhedra. But the embeddings are non-trivially tangled. Some examples are self-entangled; others are multi-component catenations. Given their maximal symmetry, these are the "simplest" polyhedral weavings. Surprisingly, nearly all of them are novel (to our knowledge). Just one example is known: Coxeter's splendid five-tetrahedron compound polyhedron, which he labelled {5,3}[5{3,3}]{3,5}.

Veronika Irvine
TesseLace
Webpage
A mathematical model for bobbin lace grounds
Bobbin lace is a 500-year-old art form in which threads are braided together in an alternating manner to produce a lace fabric. A key component in its construction is a small pattern, called a bobbin lace ground, that can be repeated periodically to fill a region of any size. I will present a mathematical model for bobbin lace grounds representing the structure as the pair (Δ1(G), ζ(v)) where Δ1(G) is a topological embedding of a 2-regular digraph, G, on a torus and ζ(v) is a mapping from the vertices of G to a set of braid words. I will describe the properties that Δ1(G) must possess in order to produce workable lace patterns. Having developed a solid, logical foundation for bobbin lace grounds, one can enumerate and exhaustively generate patterns that conform to that model. One of the key properties identified in the model is that it must be possible to partition Δ1(G) into a set of osculating circuits such that each circuit has a wrapping index of (1,0); that is, the circuit wraps once around the meridian of the torus and does not wrap around the longitude. I have used this property to exhaustively generate workable patterns for increasing numbers of vertices in G by gluing together lattice paths in an osculating manner. This produced over 5 million lace patterns from a relatively small grid size. To draw out some of the more aesthetically interesting cases for lacemakers to work on, I also looked for examples that have a high degree of symmetry and demonstrated, by computational generation, that there are lace ground representatives from each of the 17 planar periodic symmetry groups. Finally, I have established the groundwork for non-periodic lace patterns and present three new quasiperiodic families of lace patterns based on Sturmian words, the Penrose tiling by thick and thin rhombs and the Ammann-bar decoration of the Penrose tiling.
Quasiperiodic bobbin lace patterns, V. Irvine, T. Biedl, C. S. Kaplan
Developing a Mathematical Model for Bobbin Lace, V. Irvine, F. Ruskey

Randall D. Kamien
University of Pennsylvania
Webpage
Scaffolds for Knitting
Doubly and triply periodic surfaces can be used as scaffolds to capture the topology of knit fabric. We discuss the construction of these scaffolds from more basic units and show how we can optimize over their geometry to inform the design of three-dimensional, self-folding knit patterns.
Vitaliy Kurlin
University of Liverpool
Webpage
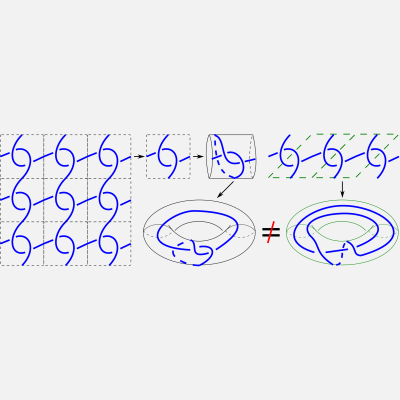
Introduction to Periodic Geometry and Topology
Periodic textiles were traditionally studied up to continuous deformations in a fixed thickened torus or with a fixed lattice basis. The more natural equivalence of textiles is a periodic isotopy whose invariants were first introduced by Morton and Grishanov. However, this branch of Periodic Topology has many more open questions than answers. The talk will focus on the related area of Periodic Geometry where the similar ambiguity of changing a lattice basis plays a key role. The key object is a periodic point set obtained by lattice translations from a finite motif of points in a unit cell. The most practical equivalence of periodic point sets is rigid motion or isometry, which preserves all interpoint distances. Real crystal structures can be reliably distinguished only by isometry invariants that should be also continuous under perturbations of points. Such recent invariants are density functions (Proceedings SoCG 2021, arXiv:2104.11046), average minimum distances (AMD, arXiv:2009.02488) and complete invariant isosets (Proceedings DGMM 2021, arXiv:2103.02749). The ultra-fast AMD enabled invariant-based visualizations of huge crystal datasets within a few hours on a modest desktop. The above work is based on joint papers with several colleagues at the Materials Innovation Factory, Liverpool, UK.
Introduction to Periodic Geometry and Topology, O. Anosova, V. Kurlin
The asymptotic behaviour and a near linear time algorithm for isometry invariants of periodic sets, D. Widdowson, M. Mosca, A. Pulido, V. Kurlin, A. Cooper
The Density Fingerprint of a Periodic Point Set, H. Edelsbrunner, T. Heiss, V. Kurlin, P. Smith, M. Wintraecken
Sonia Mahmoudi
Tohoku University
Webpage
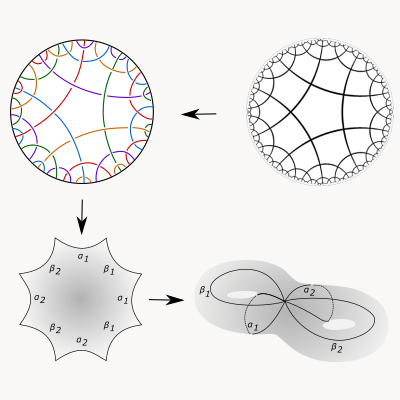
Introduction to the definition, construction and classification of weaves
From innovative woven artificial muscles to garments made from traditional woven fabrics, weavings are historically well-known structures, and still represent a very active research topic in materials science. The study of weaves as new mathematical objects is very interesting in itself but also as an interdisciplinary subject, with the aim of better understanding their geometric and topological structure, often associated with physical properties. This talk attempts to introduce weaves from a formal mathematical point of view. First, we will define Euclidean and hyperbolic weaves and state a new construction methodology. Next, an idea of classification will be discussed.
Tait's First and Second Conjectures for Weaving Diagrams, S. Mahmoudi

Sabetta Matsumoto
Georgia Institute of Technology
Webpage
Twisted topological tangles or: the knot theory of knitting
Imagine a 1D curve, then use it to fill a 2D manifold that covers an arbitrary 3D object – this computationally intensive materials challenge has been realized in the ancient technology known as knitting. This process for making functional materials 2D materials from 1D portable cloth dates back to prehistory, with the oldest known examples dating from the 11th century CE. Knitted textiles are ubiquitous as they are easy and cheap to create, lightweight, portable, flexible and stretchy. As with many functional materials, the key to knitting’s extraordinary properties lies in its microstructure.

Hugh Morton
University of Liverpool
Webpage
Capturing the topology of periodic textile patterns
I will discuss the use of diagrams on a torus in giving a compact description of a range of woven and knitted textile patterns. Following work with S. Grishanov I will show how the multi-variable Alexander polynomial can be used to calculate and display invariants of a pattern. Features of the polynomial mean that it can handle changes of scale, and it can also retrieve underlying geometric information. I will comment on some of these advantages, and also on some shortcomings.
Doubly periodic textile patterns, H. R. Morton, S. Grishanov
Vuong M. Ngo & Mohand Tahar Kechadi
Trinity College Dublin & University College Dublin
Email ; Webpage
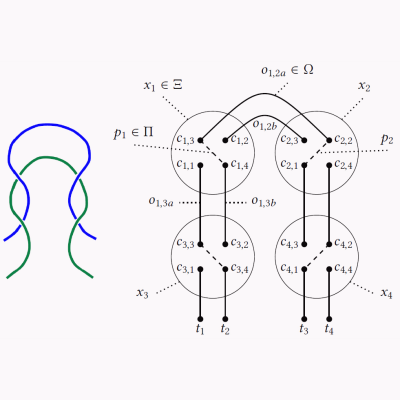
Structural textile pattern recognition and processing based on hypergraphs
To facilitate the clustering and search textiles at the level of thread structure, we introduce an approach for recognising similar weaving patterns based on their structures for textile archives. We first represent textile structures using hypergraphs and extract multisets of k-neighbourhoods describing weaving patterns from these graphs. Then, for retrieval, the resulting multisets are compared and ranked by various distance measures. While, for clustering, the multisets are clustered using various distance measures and various clustering algorithms.
Structural textile pattern recognition and processing based on hypergraphs, V. M. Ngo et al., Information Retrieval Journal, 24 (2021), 137–173.
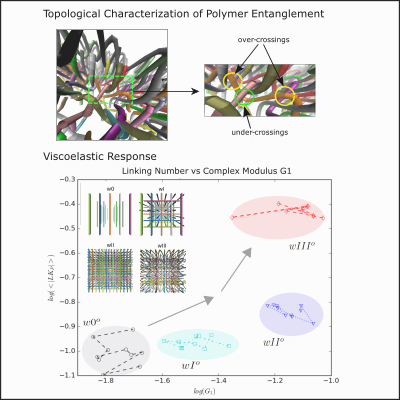
Eleni Panagiotou
University of Tennessee
Webpage
Effects of entanglement in mechanical properties of material
Material composed by entangled filamentous structures (like textiles, polymers and metal wires) exhibit complex mechanical properties. Modeling of such systems usually includes Periodic Boundary Conditions (PBC). To measure entanglement in PBC, we use the periodic linking number. We show that the periodic linking number correlates with the mechanical response of these systems. To account for multi-chain entanglement, we introduce the Jones polynomial in PBC and discuss its properties. A problem with applying the Jones polynomial to physical systems is that its calculation is computationally expensive. We discuss how Vassiliev measures and Vassiliev invariants can provide efficient alternatives.

Jessica S. Purcell
Monash University
Webpage
Geometry of biperiodic alternating links
A biperiodic alternating link is a link in the plane that has a quotient that is an alternating link in the thickened torus; the infinite weave is an example of such a link. We consider invariants of these links using hyperbolic geometry. We present a family of such links, called semi-regular links, that have their hyperbolic geometry completely determined by a Euclidean tiling. In this talk, we will describe the links and their underlying hyperbolic geometry. This is joint work with Abhijit Champanerkar and Ilya Kofman.

Koya Shimokawa
Saitama University
Webpage
3-dimensional topology and polycontinuous pattern
We study polycontinuous patterns that appear as microphase separation in block copolymers using the 3-dimensional topology. A triply periodic pattern gives a handlebody decomposition of the 3-dimensional torus. We will discuss a characterization of handlebody decompositions of the 3-dimensional torus.